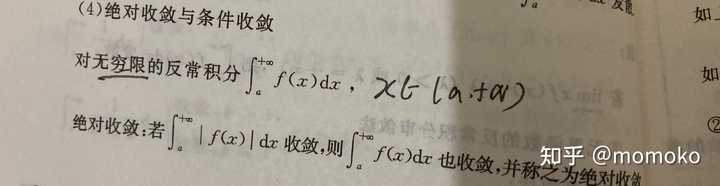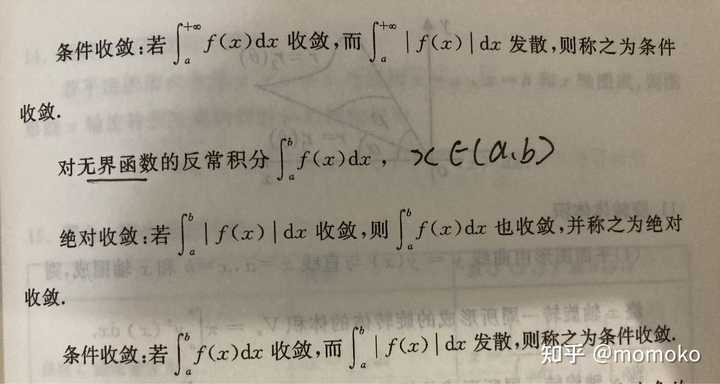如何判断反常积分的敛散性?

有很多同学问我，这万能公式在有些反常积分中并不适用，显然，你对此万能公式理解的太不到位了！我之所以这么写是因为这样已经是比较好用的简洁归纳了，实际上，为了保证证明的一致性，最为简洁的反常积分万能公式，只有一个即

任意的反常积分（包括瑕积分和无穷区间的反常积分）均可化为 \int_{}^{}\frac{1}{x^{\alpha}ln^{\beta}x}dx ，

当 且仅当 x\rightarrow 0(瑕积分)，\begin{cases} \alpha<1 \\[2ex] \alpha=1，\beta>1\end{cases},收敛

反常积分的敛散性判别在考研数学中主要是以选择题的形式出现，但我发现很多同学在遇到较复杂的反常积分，或者含参积分并不会做题，根据现有的教材普遍有定义法、比较审敛法的极限形式等等方法，小题大作，甚至有的同学在看到解析后仍是一头雾水，如何归纳出简介快速有效的判敛方法至关重要！有鉴于此，在这里我们给出一个关于反常积分的小总结（ 反常积分敛散性万能公式 ），让你能够面对反常积分快速判断出来！

首先给定以下例题进行示例，并比较常规做法，与万能公式法之间的区别：

1.判别 \int_{2}^{3}\frac{1}{(x-1)^{4}\sqrt{x(x-2)}}dx 的敛散性。

2.设 m，n 为正整数，则反常积分 \int_{0}^{1}\frac{\sqrt[m]{ln^{2}(1-x)}}{\sqrt[n]{x}}dx 的敛散性。

3.设 m，n 为常数，若反常 x\rightarrow 0 积分 \int_{0}^{+\infty}\frac{x^{n}(1-e^{-x})}{(1+x)^{m}}dx 收敛，则 m,n 的取值范围。

4.若反常积分 \int_{0}^{1}x^{a}(1-x)^{b}lnxdx 收敛，则可确定 a、b 。

5.设 a>0,f(x)=\begin{cases}\frac{arctanx}{x^{\frac{a+1}{2}}},0<x<1\\[2ex] \frac{ln(1+sin\frac{1}{x^{a}})}{x^{b}lncos\frac{1}{x}},1\leq x <+\infty \end{cases} ,若 \int_{0}^{+\infty}f(x)dx 收敛，则 a,b 的取值范围。

一、万能公式

将任意反常积分化为标准型 \int_{}^{}\frac{1}{x^{\alpha}ln^{\beta}x}dx ，
（1）当 x\rightarrow 0(瑕积分)，\begin{cases} \alpha<1 \\[2ex] \alpha=1，\beta>1\end{cases},收敛 ；
（2）当 x\rightarrow \infty(无穷区间的反常积分)，\begin{cases} \alpha>1 \\[2ex] \alpha=1，\beta>1\end{cases},收敛
（3）其他情况均发散！
（注意：此公式推导可参照我的14节课冲刺课，实际上，记住结论即可）

二、例题示范

1.判别 \int_{2}^{3}\frac{1}{(x-1)^{4}\sqrt{x(x-2)}}dx 的敛散性。

万能公式法：

当 x\rightarrow2^{+} 时，
\frac{1}{(x-1)^{4}\sqrt{x(x-2)}}\sim\frac{1}{\sqrt{2}\sqrt{x-2}} ，
因 \alpha=\frac{1}{2}<1 ,故 收敛。

2.设 m，n 为正整数，则反常积分 \int_{0}^{1}\frac{\sqrt[m]{ln^{2}(1-x)}}{\sqrt[n]{x}}dx 的敛散性。

万能公式法;

当 x\rightarrow0^{+} 时，有
\frac{\sqrt[m]{ln^{2}(1-x)}}{\sqrt[n]{x}}=\frac{1}{x^{\frac{1}{n}}ln^{-\frac{2}{m}}(1-x)}\sim\frac{1}{x^{\frac{1}{n}-\frac{2}{m}}} ,
因， \frac{2}{m}>0,\frac{1}{n}<1, 所以 \alpha=\frac{1}{n}-\frac{2}{m}<1, 显然关于 x=0 的瑕积分收敛；
当 x\rightarrow1^{-} 时，有 \frac{\sqrt[m]{ln^{2}(1-x)}}{\sqrt[n]{x}}=\frac{1}{x^{\frac{1}{n}}ln^{-\frac{2}{m}}(1-x)}\sim\frac{1}{(1-x)^{0}ln^{-\frac{2}{m}}(1-x)}
由于 \alpha=0<1 ,显然，关于 x=1 的瑕积分收敛；
综上所述，任意正整数 m，n 均使得反常积分 \int_{0}^{1}\frac{\sqrt[m]{ln^{2}(1-x)}}{\sqrt[n]{x}}dx 收敛。

3. 设 m，n 为常数，若反常积分 \int_{0}^{+\infty}\frac{x^{n}(1-e^{-x})}{(1+x)^{m}}dx 收敛，则 m,n 的取值范围。

万能公式法：

当 x\rightarrow0^{+} 时，有
\frac{x^{n}(1-e^{-x})}{(1+x)^{m}}\sim\frac{1}{x^{-(n+1)}}
若关于 x=0 的瑕积分收敛，则 \alpha=-(n+1)<1, 即 n>-2 ；

当 x\rightarrow+\infty 时，有
\frac{x^{n}(1-e^{-x})}{(1+x)^{m}}\sim\frac{1}{x^{m-n}}
若关于无穷区间的反常积分收敛，则 \alpha=m-n>1, 即 m>n+1 ；
综上所述，当 n>-2 ， m>n+1 时 使得反常积分 \int_{0}^{+\infty}\frac{x^{n}(1-e^{-x})}{(1+x)^{m}}dx 收敛。

4. 若反常积分 \int_{0}^{1}x^{a}(1-x)^{b}lnxdx 收敛，则可确定 a、b 。

万能公式法：

当 x\rightarrow0^{+} 时，有
x^{a}(1-x)^{b}lnx\sim\frac{1}{x^{-a}ln^{-1}x}
若关于 x=0 的瑕积分收敛，则 \alpha=-a<1, 即 a>-1 ；
当 x\rightarrow1^{-} 时，有
x^{a}(1-x)^{b}lnx\sim-\frac{1}{(1-x)^{-(b+1)}}
若关于 x=1 的瑕积分收敛，则 \alpha=-(b+1)<1, 即 b>-2 ；
综上所述，当 a>-1 ， b>-2 时 使得反常积分 \int_{0}^{1}x^{a}(1-x)^{b}lnxdx 收敛。

5.设 a>0,f(x)=\begin{cases}\frac{arctanx}{x^{\frac{a+1}{2}}},0<x<1\\[2ex] \frac{ln(1+sin\frac{1}{x^{a}})}{x^{b}lncos\frac{1}{x}},1\leq x <+\infty \end{cases} ,若 \int_{0}^{+\infty}f(x)dx 收敛，则 a,b 的取值范围。

万能公式法：

当 x\rightarrow0^{+} 时，有
\frac{arctanx}{x^{\frac{a+1}{2}}}\sim\frac{1}{x^{\frac{a-1}{2}}}
若关于 x=0 的瑕积分收敛，则 \alpha=\frac{a-1}{2}<1, 即 a<3 ；
当 x\rightarrow+\infty 时，有
\frac{ln(1+sin\frac{1}{x^{a}})}{x^{b}lncos\frac{1}{x}}\sim-\frac{2}{x^{a+b-2}}
若关于无穷区间的反常积分收敛，则 \alpha=a+b-2>1, 即 a+b>3 ；
综上所述，当 a<3 , a+b>3 时使得反常积分 \int_{0}^{+\infty}f(x)dx 收敛。

三、反常积分与无穷级数的关系

在这里，我们给出了一个很好用的万能公式，那么是否囊括的足够全呢？或者说所有的反常积分都适合吗？

不妨，再给出一个迥然不同的例子：

6.若反常积分 \int_{0}^{+\infty}e^{-ax}cosbxdx 收敛，求 a，b 取值范围。

常规做法（分类讨论）：

（1）当 a=b=0 时，反常积分为 \int_{0}^{+\infty}1dx ，发散；
（2）当 a=0,b\ne0 时，反常积分为 \int_{0}^{+\infty}cosbxdx=\frac{sinbx}{b}丨_{0}^{+\infty} ，发散；
（3）当 a\ne0,b=0 时，反常积分为 \int_{0}^{+\infty}e^{-ax}dx
a.若 a>0 ,则反常积分 \int_{0}^{+\infty}e^{-ax}dx=-\frac{e^{-ax}}{a}=\frac{1}{a} ,收敛；
b.若 a<0 ,则反常积分 \int_{0}^{+\infty}e^{-ax}dx 发散。
（4）当 a\ne0,b\ne0 时，区间再现，有
\int_{0}^{A}e^{-ax}cosbxdx=\frac{e^{-aA}}{a^2+b^2}(bsinbA-acosbA)+\frac{a}{a^2+b^2}
a.若 a>0 ,则反常积分 \lim_{A \rightarrow +\infty}[{x}\frac{e^{-aA}}{a^2+b^2}(bsinbA-acosbA)+\frac{a}{a^2+b^2}]=\frac{a}{a^2+b^2} ,收敛；
b.若 a<0 ,则反常积分
\lim_{A \rightarrow +\infty}[{x}\frac{e^{-aA}}{a^2+b^2}(bsinbA-acosbA)+\frac{a}{a^2+b^2}] 不存在，发散。
综上所述，当 a>0,b 任意时，反常积分收敛。

极简做法（向无穷级数看齐）：

将其作为连续型的无穷级数看待，则根据无穷级数收敛性质可知，令
\lim_{x \rightarrow +\infty}{}u_{x}=\lim_{x \rightarrow +\infty}{}e^{-ax}cosbx=0 时级数收敛的必要条件，因此，当 a>0,b 任意时， \lim_{x \rightarrow +\infty}{}u_{x}=0 ，显然，此时，级数必收敛，结果易得。

从这里，我们引出了关于无穷级数的敛散性判别，这又是另一个万能公式的开始了！具体请参照14课冲刺课或我的专栏 考研数学如何取得145+的分数？ ！