1、女士的身高-体重例子。–借助excel数据分析功能
使用excel中散点图功能将数据绘制成散点图。

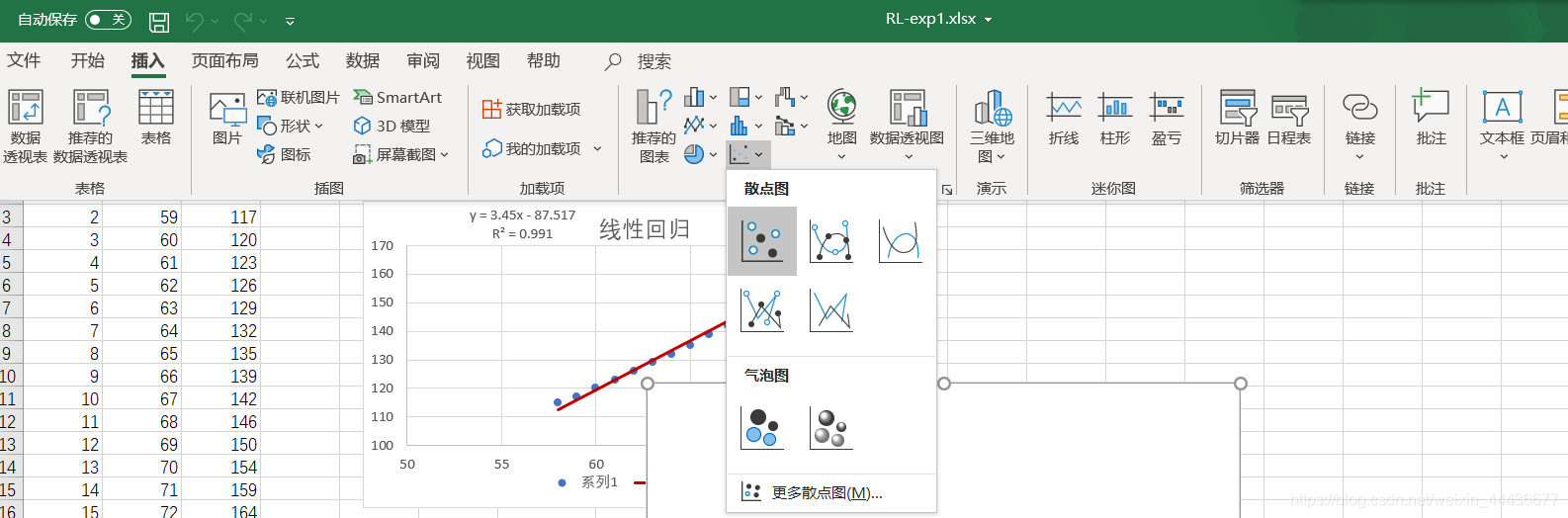
散点图右键，选择“设置趋势线格式”。

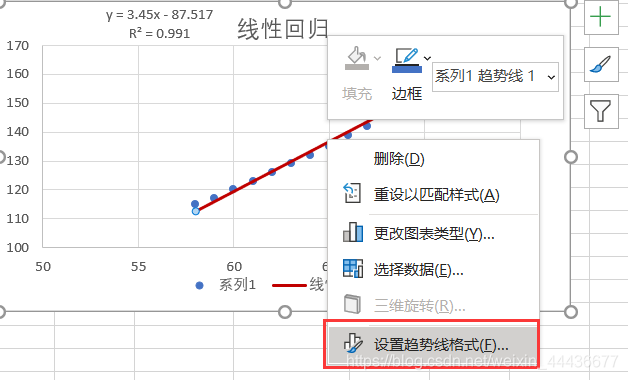
弹出的设置框可以设置散点图样式，趋势线选择线性，勾选显示公式、显示R平方值。

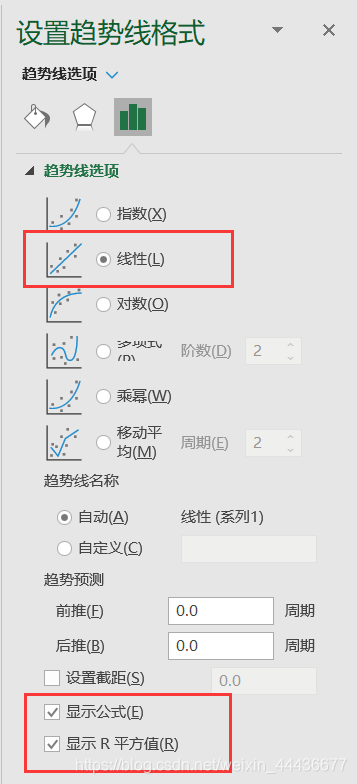
同样的，在坐标轴右键，选择“设置坐标轴格式”。弹出的设置框可以修改一下坐标轴的初始值，让散点图更好看一些。

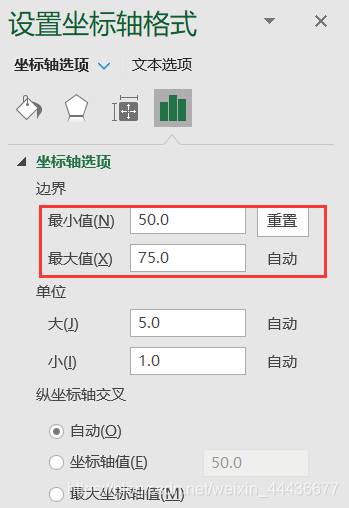
最终散点图如下。可以看到数据分布特征非常明显，呈现线性分布。右键添加趋势线，并显示方程、R²。R²=0.991，接近于 1，说明模型能够解释99.1%的方差，效果非常好。

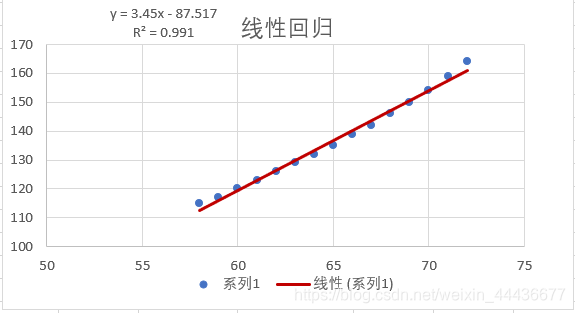
根据excel中：“数据-数据分析-回归”得到得模型如下。
旧版excel点击：“工具-数据-数据分析-回归”。

Y值输入区域：选择你的Y值数据，我这为C列；X值输入区域：选择你的X值数据，我这为B列。
输出区域默认为新的工作表，但我希望输出与数据在同一张表格，所以选择了想要的区域位置。其他的内容根据需要自行勾选。

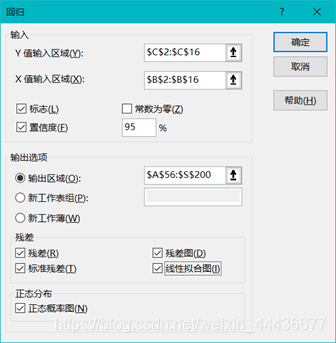
输出内容如下：

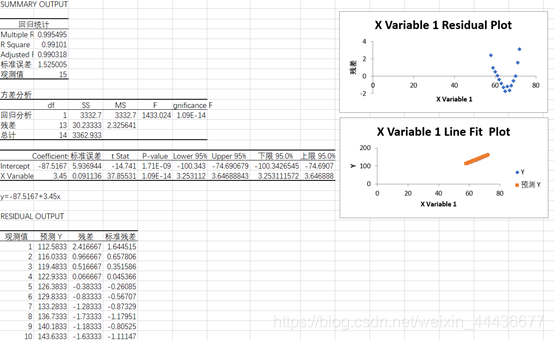
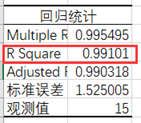
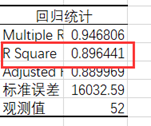
这个值为R²，反映了模型的解释能力，越接近于1说明效果越好。这里可以看出我们模型的效果很好。

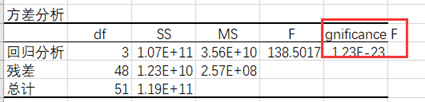
F检验，即对方程是否有线性关系的检验，原假设 H0：方程没有线性关系，我们看到 P值< 0.01，故拒绝 H0，认为方程具有线性关系。

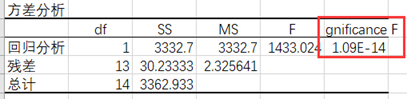
t 检验，即对一元线性方程的截距项α和系数β进行检验，H0：α=0，可以看到 P<0.01，拒绝H0，说明α通过了t检验；同理，β也通过了 t检验。

根据这里可以得到线性回归方程为y=-87.5167+3.45x。
方程是需要自己写的哈，数据分析功能不会直接输出的。

残差图：可以看到数据并没有散乱的分布在X 轴两侧，而是呈抛物线的形状，说明模型中需要引入一个二次项，从散点图中亦可以看出。

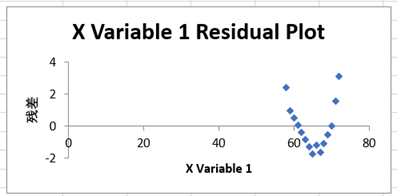
正态概率图：散点分布在一条直线上，说明服从正太分布。当样本足够大（一般认为≥30）时，一般不需要太关注正太分布性。

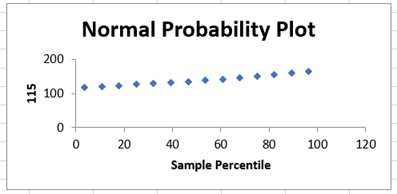
2、气温-冰红茶销售量例子。–直接计算
使用excel中散点图功能将数据绘制成散点图。可以看到数据呈现线性分布，气温与销售量呈正相关。右键添加趋势线，并显示方程、R²。R²接近于 1，说明模型效果较好。

第A列为每日最高气温x的值，A16为x的和，A17为x的平均数。第B列为当日冰红茶的销售量y，B16为y的和，B17为y的平均数。第C列为各个x减去x平均值的具体数值。第E列为的各个x的离差平方，E16即为x的离差平方和Sxx的值。第D列为各个y减去y平均值的具体数值。第F列为的各个y的离差平方，F16即为y的离差平方和Syy的值。第G列为的各个x与相应y的离差平方，G16即为x和y的离差平方和Sxy的值。

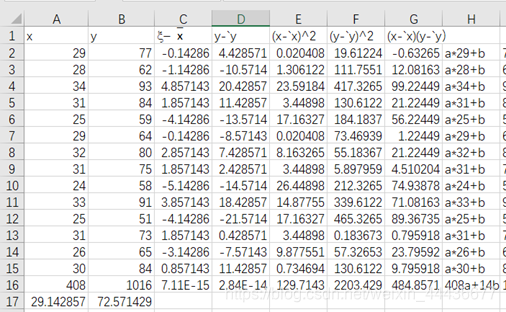
由a=Sxy/Sxx得到a的值，由b=y-ax得到b的值。然后得出方程y=3.7x-36.4。

根据公式得到销售量的预测值，即第K列。K16为预测值的和，K17为预测值的平均数。第L列为预测值减去预测平均数的具体数值。第M列为预测值的离差平方，M16即为预测值的离差平方和。第N列为y与预测值的离差平方，N16为y和预测值的离差平方和。

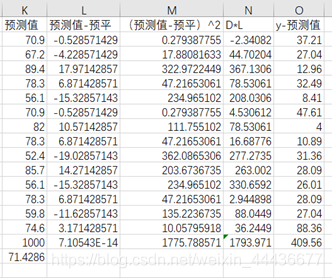
由R2=Syy2/sqrt(Syy*Syy1)得到R2.。可见该方程的精度比较高。

3、薪资-性别-年龄-教育程度例子。–借助excel数据分析功能
根据excel中散点图功能，绘制出三个自变量与因变量的散点图，并得到方程和R²。可以看出年龄、工龄、教育程度与薪资都成正相关。
其中年龄-薪资的模型图拟合度较好，R²最大。
做法同1类似，需要分别选择X值。

同1的步骤，根据excel中：“数据-数据分析-回归”得到得模型如下。
注意：x的赋值要把三个x都选上。输出内容如下：

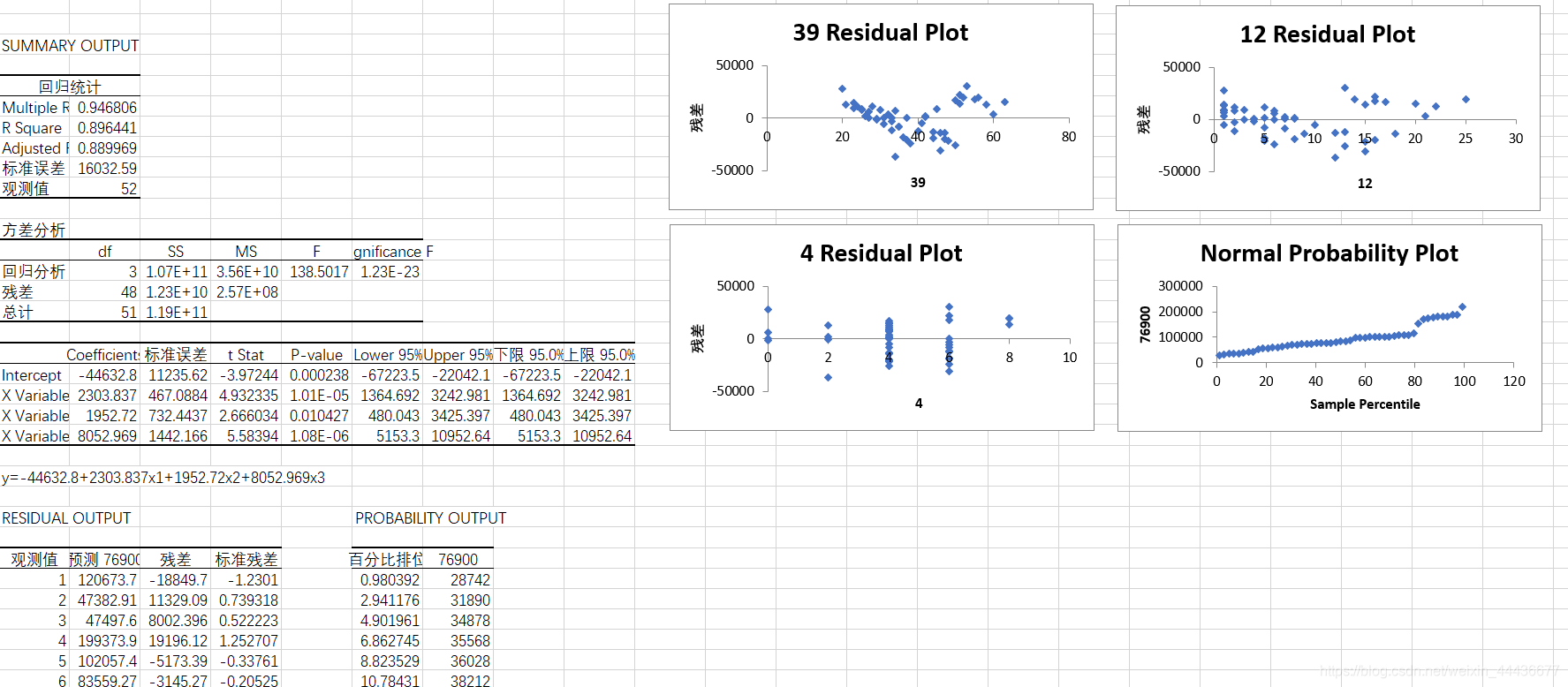
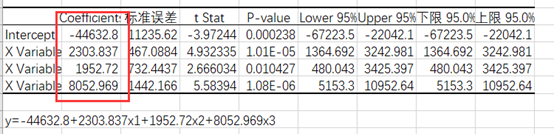
整体的R²，可以看出我们模型的效果还是比较好的。

整体方程P值<<0.01，故拒绝原假设，方程通过了F检验。

所有的自变量都通过了t检验。

可以得到线性回归方程为
y=-44632.8+2303.837x1+1952.72x2+8052.969x3。

4、店铺营业额-店铺面积-离车站距离例子。–直接计算
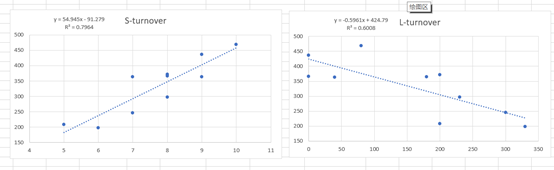
使用excel中散点图功能将数据绘制成散点图。可以看到数据呈现线性分布，店铺面积与营业额呈正相关，距离与营业额呈负相关。。

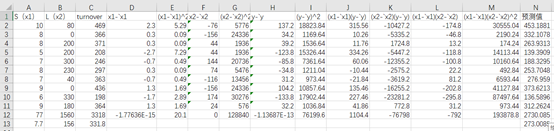
第A列为店铺的面积大小（x1），A12为面积大小之和，A13为面积的平均值。第B列为店铺到车站的距离（x2），B12为距离之和，B13为距离的平均数。第C列为营业额的数值（y），C12为营业额之和，C13为营业额的平均数。第D列为各个x1减去x1平均值的具体数值。第E列为的各个x1的离差平方，E12即为x1的离差平方和Sx1x1的值。
第F列为各个x2减去x2平均值的具体数值。第G列为的各个x2的离差平方，G12即为x2的离差平方和Sx2x2的值。第H列为各个y减去y平均值的具体数值。第I列为的各个y的离差平方，I12即为y的离差平方和Syy的值。第J列为的各个x1与相应y的离差平方，J12即为x1和y的离差平方和Sx1y的值。第K列为的各个x2与相应y的离差平方，K12即为x2和y的离差平方和Sx2y的值。第L列为的各个x1与相应x2的离差平方，L12即为x1和x2的离差平方和Sx1x2的值。第N列为预测值。

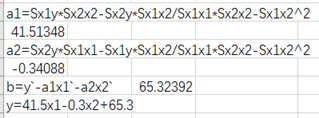
由a1=Sx1y Sx2x2-Sx2y Sx1x2/Sx1x1 Sx2x2-Sx1x2^ 2得到a1的值，由a2=Sx2y Sx1x1-Sx1y Sx1x2/Sx1x1 Sx2x2-Sx1x2^2得到a2的值，由b=y -a1x1 -a2x2`得到b值，最后得到方程y=41.5x1-0.3x2+65.3。