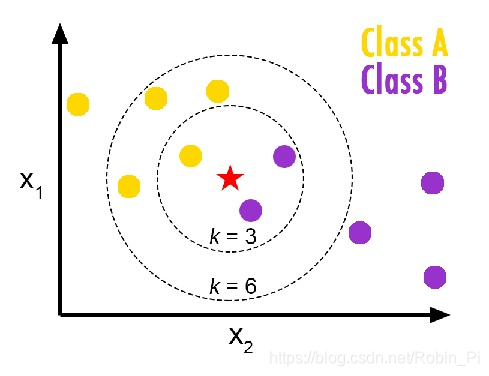
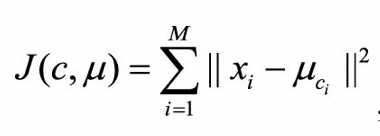相关文章推荐
|
|
豁达的帽子 · 什么是机器学习(ML) | ...· 2 月前 · |
|
|
有腹肌的斑马 · Appium微信小程序自动化之开启webvi ...· 2 天前 · |
|
|
豁达的香蕉 · MATLAB Onramp | ...· 5 月前 · |
|
|
无邪的黄花菜 · 张一鸣10年的微博汇总!· 6 月前 · |
|
|
冷冷的滑板 · 七品芝麻官_百度百科· 1 年前 · |
|
|
淡定的斑马 · 智能机顶盒怎么连接wifi_什么值得买· 2 年前 · |
|
|
月球上的西红柿 · 中俄交通大学联盟_百度百科· 2 年前 · |
推荐文章
|
|
无邪的黄花菜 · 张一鸣10年的微博汇总! 6 月前 |
|
|
冷冷的滑板 · 七品芝麻官_百度百科 1 年前 |
|
|
淡定的斑马 · 智能机顶盒怎么连接wifi_什么值得买 2 年前 |
|
|
月球上的西红柿 · 中俄交通大学联盟_百度百科 2 年前 |