数学知识整理：二重积分

相关文章推荐

纯真的生姜 · 第一类曲线积分的基本计算方法-百度经验· 6 月前 ·

纯真的生姜 · 第一类曲线（曲面）积分的理解与计算- ...· 6 月前 ·

纯真的生姜 · 第一型曲线积分_百度百科· 6 月前 ·

纯真的生姜 · 多变量微积分笔记10——二重积分的应用- ...· 6 月前 ·

纯真的生姜 · 数学知识整理：二重积分-CSDN博客· 6 月前 ·

本文详细探讨了二重积分的性质，包括可积性条件、线性性质、积分区域可加性及积分不等式。此外，介绍了二重积分的计算方法，如按区域和形状分类、利用奇偶性简化计算，并通过实例解析如何转换坐标进行积分。同时，阐述了二重积分与极坐标之间的转换，并讨论了换元法在二重积分计算中的应用。摘要生成于，由 DeepSeek-R1 满血版支持，

当区域D关于x轴对称时
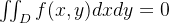- · $\iint_Df(x,y)dxdy=0$ ,f(x,y)是奇函数
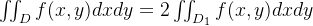- $\iint_{D}f(x,y)dxdy=2\iint_{D_1}f(x,y)dxdy$ ，f(x,y)是偶函数，且D1是D的上半平面或者下半平面
当区域D关于y轴对称时
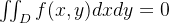- · $\iint_Df(x,y)dxdy=0$ ,f(x,y)是奇函数
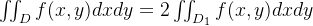- $\iint_{D}f(x,y)dxdy=2\iint_{D_1}f(x,y)dxdy$ ，f(x,y)是偶函数，且D1是D的左半平面或者右半平面
当区域D关于x轴，y轴都对称时
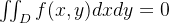- · $\iint_Df(x,y)dxdy=0$ ,f(x,y)是奇函数
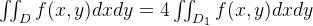- $\iint_{D}f(x,y)dxdy=4\iint_{D_1}f(x,y)dxdy$ ，f(x,y)是偶函数，且D1是D在任一象限中的部分

1.2.3 举例

设函数f(x,y)在有界闭区域D上连续，如果变换 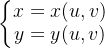$\left\{\begin{matrix} x=x(u,v)\\ y=y(u,v) \end{matrix}\right.$ 满足以下三个条件

将uv平面上区域D'一一对应到xy平面上的D
变换函数x(u,v),y(u,v)在D'上连续，且有连续的一阶偏微商
雅可比行列式 $J(u,v)=\begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} \end{vmatrix}$ 在D'上不取零值

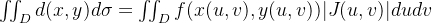
则有换元公式 $\iint_Dd(x,y)d\sigma=\iint_Df(x(u,v),y(u,v))|J(u,v)|dudv$

注：可以证明上述三个条件可以适当地放宽：对于（1）和（3），可以允许个别点/个别曲线上不满足；对于（2），可以允许分段连续

4.1 举例

求二重积分 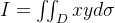$I=\iint_D xy d\sigma$ 其中区域D是由抛物线 $y^2=x,y^2=4x,x^2=y,x^2=4y$ 围成的

二重积分 1. 定义附录附录1. 二重积分 1. 定义 z=f(x,y)vol=∬Rf(x,y)dAvol=∫xminxmaxS(x)dxFor given x, S(x)=∫ymin(x)ymax(x)f(x,y)dy⇒vol=∫xminxmax∫ymin(x)ymax(x)f(x,y)dydx z=f(x,y) \quad \text{vol}=\iint_{R}{f(x,y)}\mathrm{d}{A} \\ \text{vol}=\int_{x_{min}}^{x_{ma

将 二重积分 与曲面柱体的体积联系，便于理解 ①（数乘）：∬Dkf(x, y)dσ = k∬Df(x, y)dσ , k为常数。 ②（加减）：∬D[f(x, y)±g(x, y)]dσ = ∬Df(x, y)dσ ± ∬Dg(x, y)dσ。 ③（区域可加性）：∬Df(x, y)dσ = ∑∬Dkf(x, y)dσ //分成多个部分。 ④（比较定理）： ⑤（估值定理）： ⑥（中值定理）： ⑦（对称性定理）：（3）计算 ①先X后Y ②先Y后X 标志：出现x2 + y

基础知识： 二重积分 的积分区域在一个平面上 1.直角投影法：分别在x轴和y轴上投影，做法一：先确定x的取值范围，然后从x的坐标区域做一条垂线交于曲线，分别得到y1(x)和y2(x)；这种积分先对x积分，再对y积分做法二：先确定y的取值范围，然后从y的坐标区域做一条垂线交于曲线，分别得到x1(y)和x2(y)，这种积分先对y积分，再对x积分 2.极坐标法：当积分区域或被积函数含有x∧2+y∧2时，使用极坐标法首先确定θ和r的取值范围，r的取值范围可以用x=rcosθ,y=rsinθ代入积分区域的函数得到

二重积分 是二元函数在空间上的积分，同定积分类似，是某种特定形式的和的极限。本质是求曲顶柱体体积。重积分有着广泛的应用，可以用来计算曲面的面积，平面薄片重心等。平面区域的 二重积分 可以推广为在高维空间中的（有向）曲面上进行积分，称为曲面积分。　　本篇涉及到的单变量积分的知识可参考《数学笔记13——定积分》 二重积分 的意义　　一元积分的被积函数是二维空间的曲线，其几何意义是计算曲线与x轴围...

论文笔记：Diff-RNTraj: A Structure-aware Diffusion Model for Road Network-constrained Trajectory Generati CSDN-Ada助手: 你好，CSDN 开始提供 #论文阅读# 的列表服务了。请看：https://blog.csdn.net/nav/advanced-technology/paper-reading?utm_source=csdn_ai_ada_blog_reply 。如果你有更多需求，请来这里 https://gitcode.net/csdn/csdn-tags/-/issues/34?utm_source=csdn_ai_ada_blog_reply 给我们提。论文笔记：Can Slow-thinking LLMs Reason Over Time? Empirical Studies in Time Series Forecasting CSDN-Ada助手: 你好，CSDN 开始提供 #论文阅读# 的列表服务了。请看：https://blog.csdn.net/nav/advanced-technology/paper-reading?utm_source=csdn_ai_ada_blog_reply 。如果你有更多需求，请来这里 https://gitcode.net/csdn/csdn-tags/-/issues/34?utm_source=csdn_ai_ada_blog_reply 给我们提。论文笔记：UniTraj: Learning a Universal Trajectory Foundation Model from Billion-Scale Worldwide Traces CSDN-Ada助手: 你好，CSDN 开始提供 #论文阅读# 的列表服务了。请看：https://blog.csdn.net/nav/advanced-technology/paper-reading?utm_source=csdn_ai_ada_blog_reply 。如果你有更多需求，请来这里 https://gitcode.net/csdn/csdn-tags/-/issues/34?utm_source=csdn_ai_ada_blog_reply 给我们提。论文笔记：MGeo: Multi-Modal Geographic Language Model Pre-Training CSDN-Ada助手: 你好，CSDN 开始提供 #论文阅读# 的列表服务了。请看：https://blog.csdn.net/nav/advanced-technology/paper-reading?utm_source=csdn_ai_ada_blog_reply 。如果你有更多需求，请来这里 https://gitcode.net/csdn/csdn-tags/-/issues/34?utm_source=csdn_ai_ada_blog_reply 给我们提。论文笔记：Answering POI-Recommendation Questions using TourismReviews CSDN-Ada助手: 你好，CSDN 开始提供 #论文阅读# 的列表服务了。请看：https://blog.csdn.net/nav/advanced-technology/paper-reading?utm_source=csdn_ai_ada_blog_reply 。如果你有更多需求，请来这里 https://gitcode.net/csdn/csdn-tags/-/issues/34?utm_source=csdn_ai_ada_blog_reply 给我们提。