高中立体几何中垂直平行判定依据
有没有人觉得这样看比较吃劲,直接白嫖拿走吧!!!!!我不要点赞啊!!!!
链接: https:// pan.baidu.com/s/1IaI6YF x3DbOw3w4cxptOZA
提取码:6666
㈠线线平行
①两直线共面且无公共点(线线平行的定义)
②同位角相等,两直线平行。
③内错角相等,两直线平行。
④同旁内角互补,两直线平行。
⑤利用相似证平行
⑥垂直于同一条直线的两直线平行(只适用于平面内)
⑦根据平行四边形性质推平行(对边平行且相等)
⑧一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线,与该直线平行。
(a∥α,a⊂β,α∩β=b ⇒ a∥b)
⑨如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
(α∥β,α∩γ=a. β∩γ=b⇒ a∥b)
⑩垂直于同一平面的两直线相互平行。
(a⊥α,b⊥α ⇒ a∥b)
㈡线面平行;
①平面外一条直线与此平面内的一条直线平行则该直线与此平面平行。
(a⊄α,b⊂α 且a∥b,a∥α)
②两个平面平行,其中一个平面内任意一条直线都平行于另一个平面。
(α∥β,a⊂α ⇒a∥β)
③平面外的两条平行线,若其中一条与这个平面平行,则另一条也与此平面平行。
(a⊄α ,b⊄α,a∥b,a(b)∥α⇒ b(a)∥α)
④两个平面互相垂直,如果其中一个平面外的一条直线垂直于另一个平面,那么这条直线和这个平面平行。
(α⊥β,l⊄α,l⊥β⇒l∥α)
⑤两平行平面外的一条直线,平行于两平行平面中的一个,那么它也平行于另外一个。
(l⊄α,l⊄β,l∥α(β),α∥β⇒l∥α)
⑥平面外的一条直线,垂直于这个平面的一条垂线,那么这条直线与这个平面平行。
(l⊄α,a⊥α,l⊥a⇒l∥α)
㈢面面平行
①一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
(l⊂α,a⊂α,l∩a=B,l∥β,a∥β⇒α∥β)
②一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
(l⊂α,a⊂α,l∩a=B,b⊂β,c⊂β,b∩c=D,l∥b,a∥c⇒α∥β)
③平行于同一平面的两平面平行。
(α∥β,γ∥β⇒α∥γ)
④垂直于同一条直线的两个平面互相平行。
(l⊥α,l⊥β⇒α∥β)
⑤如果两个平面的两条垂线互相平行,则这两个平面互相平行。
(l⊥α,a⊥β,l∥a⇒α∥β)
㈣线线垂直
①线面垂直则这条直线垂直于平面内的任意一条直线。
(l⊥α,b⊂α⇒l⊥b)
②一条直线垂直于两条平行线中的一条,则它也垂直于另一条。
(a∥b,c⊥a(b)⇒c⊥b(a))
③两条平行线中的一条直线,垂直于某个平面内的一条直线,则另一条直线也垂直于这条直线。
(a∥b,a(b)⊥c⇒b(a)⊥c)
④【三垂线定理】平面内的一条直线,如果与穿过这个平面的一条斜线在这个平面上的射影垂直,那么它也和这条斜线垂直。(可逆)
有图
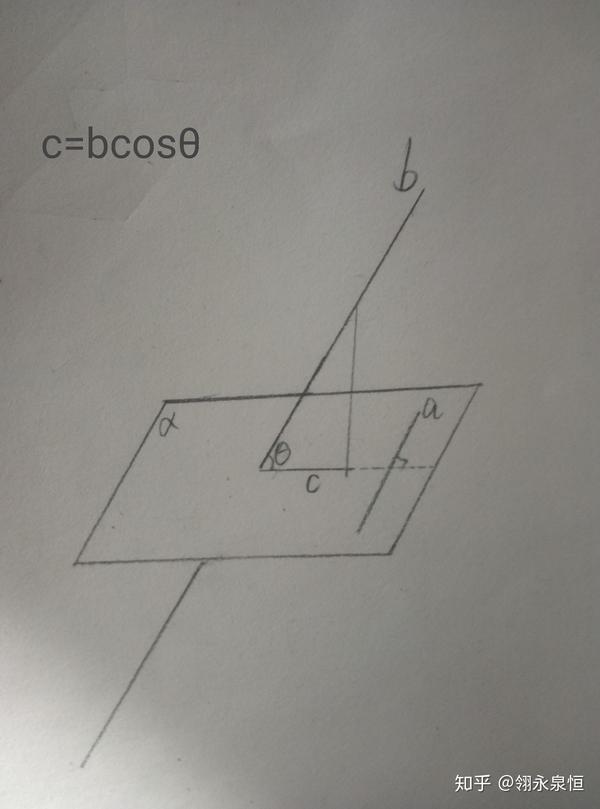
⑤三角形相似。
⑥勾股定理。
⑦菱形◇对角线垂直。
⑧直径所对圆周角是直角。
㈤线面垂直
①一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
(l⊥m,l⊥n,m∩n=A,m⊂α,n⊂α⇒l⊥α)
②两个平面垂直,则其中任一平面内垂直于交线的直线都与另一平面垂直。
(α⊥β,α∩β=A,b⊂β,b⊥a⇒b⊥α)
③如果两个相交平面都垂直于第三个平面,那么它们的交线也垂直于第三个平面。
(α∩β=l,α⊥γ,β⊥γ⇒l⊥γ)
④一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个。
(α∥β,l⊥α(β)⇒l⊥β(α))
⑤两条平行线中的一条垂直于某个平面,则另一条也垂直于这个平面。
(a∥b,a(b)⊥α⇒b(a)⊥α)
㈥面面垂直(二面角为90º)
①一个平面过另一个平面的垂线,则这两个平面垂直。
(a⊥α,a⊂β⇒α⊥β)
②一条直线和一个平面平行,若这条直线和另一个平面垂直,则这两个平面垂直。
(a∥α,a⊥β⇒α⊥β)
③如下图↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓

④利用空间向量证明面面垂直。
⑤如果两个平面相交,如果它们所成的二面角为90°,则证明这两个平面互相垂直。
【补充:】【空间几何中常用概念补充:】
㈠等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
㈡三角形的五心
1.重心:三角形中,三条中线的交点。
【三角形重心的性质:】
①角与重心的连线把三角形分成面积相等的两半。
②角与重心的连线把对边分成相等的两半。
③三条中线把三角形分成六个面积相等的三角形。
④重心把中线分成2/3与1/3两段。
2.垂心:三角形中,三条高的交点。
【三角形垂心的性质:】
①锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外.
②三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;
③垂心H关于三边的对称点,均在△ABC的外接圆上.
④ △ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AH·HD=BH·HE=CH·HF.
⑤ H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组).
⑥ △ABC,△ABH,△BCH,△ACH的外接圆是等圆.
⑦ 在非直角三角形中,过H的直线交AB、AC所在直线分别于P、Q,则 AB/AP·tanB+AC/AQ·tanC=tanA+tanB+tanC.
⑧ 设O,H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA.
⑨ 锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍.
⑩ 锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短.
⑪设锐角△ABC内有一点P,那么P是垂心的充分必要条件(PB*PC*BC+PB*PA*AB+PA*PC*AC=AB*BC*CA)
⑫设H为非直角三角形的垂心,且D、E、F分别为H在BC,CA,AB上的射影,H1,H2,H3分别为△AEF,△BDF,△CDE的垂心,则△DEF≌△H1H2H3.
⑬三角形垂心H的垂足三角形的三边,分别平行于原三角形外接圆在各顶点的切线.
3.内心:三角形中,三条角平分线的交点 (即三角形内切圆的圆心)
4.外心:三角形中,三条垂直平分线的交点。(即三角形外接圆的圆心)
5.旁心:旁心是三角形两条外角平分线和一条内角平分线的交点,它到三边的距离相等。
㈢直三棱柱:直三棱柱是各个侧面的高相等,底面是三角形,上表面和下表面平行且全等,所有的侧棱相等且相互平行且垂直于两底面的棱柱。上下表面三角形可以是任意三角形。
㈣正三棱柱:正三棱柱是直三棱柱的特殊情况,即上下面是正三角形。
㈤正三棱锥:正三棱锥是锥体中底面是正三角形,三个侧面是全等的等腰三角形的三棱锥。
㈥正四面体:正四面体必须每个面都是全等的等边三角形的四面体。
