gray_lap = cv2.Laplacian(img,cv2.CV_16S,ksize = 3)    
# 转回uint8
dst = cv2.convertScaleAbs(gray_lap) 
                    拉普拉斯算子Laplace概述算子模板应用原理opencv代码效果展示概述定义：拉普拉斯算子是n维欧几里德空间中的一个二阶微分算子，定义为梯度（▽f）的散度（▽·f），函数  f 的拉普拉斯算子▽2f 又可以写成▽·▽f。拉普拉斯算子是一种各向同性微分算子，它具有旋转不变性。一个二维图像函数的拉普拉斯变换是各向同性的二阶导数。求导阶数：二阶求导。拉普拉斯算子 (Laplace) 作用：1.对图像进行边缘检测；2.锐化图像；3.判断模糊。算子模板邻域系统是4或8邻域的Laplacian 
				
拉普拉斯算子（Laplace Operator）
拉普拉斯算子（Laplace Operator）为标量算子（a scalar operator）：两个梯度向量算子（gradient vector operator）的内积（dot product，inner product）
Δ=∇⋅∇=∇2=[∂∂x1⋯∂∂xN][∂∂x1⋮∂∂xN]=∑n=1N∂2∂xn2\Delta = \nabla \c...
Laplace算子作为边缘检测之一，和Sobel算子一样也是工程数学中常用的一种积分变换，属于空间锐化滤波操作。拉普拉斯算子（Laplace Operator）是n维欧几里德空间中的一个二阶微分算子，定义为梯度（▽f）的散度（▽·f）。
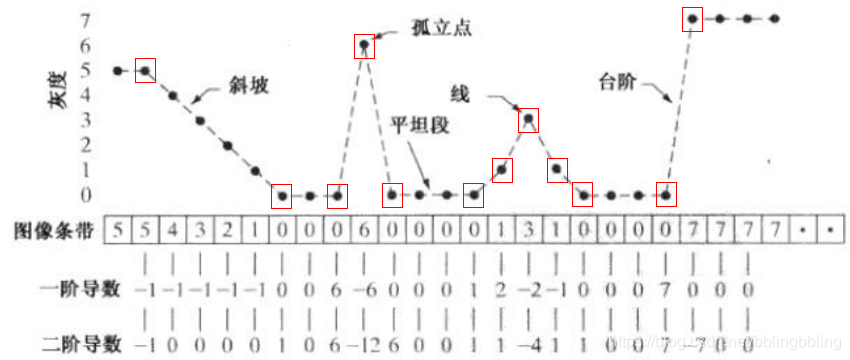
拉普拉斯算子是二阶微分线性算子，在图像边缘处理中，二阶微分的边缘定位能力更强，锐化效果更好，因此在进行图像边缘处理时，直接采用二阶微分算子而不使用一阶微分。
图1 一阶微分和二阶微分计算图
离散函数的导数退化成了差分，一维一阶差分公式和二阶差分公式分别为：
1、图像检测的原理。
    图像检测的原理是检测相邻的几个点像素值之间的变化率，相对于对函数求导。求点P(x,y)的变换率，可以在点P周围选取一些点，求x方向的距离Gx，再求y方向上的距离Gy。最后变换率G等于Gx平方加上Gy平方的和的平方差，即G=Math.sqrt(Gx^2+Gy^2)。
2、Laplacian算子。
    拉普拉斯算子对...
  在一维连续数集上有函数f(x),我们可以通过求导获得该函数在任一点的斜率，根据导数的定义有：
  在二维连续数集上有函数f(x,y),我们也可以通过求导获得该函数在x和y分量的偏导数，根据定义有：
二、Prewitt算子和Sobel算子
  Prewitt算子是一种一阶微分算子的边缘检测，利用像素点上下、左右邻点的灰度差，在边缘处达到极值检测边缘，去掉部分伪边缘，对噪声具有平...
% 拉普拉斯算子锐化滤波
laplacian_filter = [0 -1 0; -1 5 -1; 0 -1 0]; % 拉普拉斯算子
filtered_img4 = imfilter(noisy_img, laplacian_filter);
% 显示结果
subplot(2, 3, 1), imshow(img), title('原始图像');
subplot(2, 3, 2), imshow(noisy_img), title('添加噪声');
subplot(2, 3, 3), imshow(filtered_img1), title('卷积滤波');
subplot(2, 3, 4), imshow(filtered_img2), title('中值滤波');
subplot(2, 3, 5), imshow(filtered_img3), title('自适应滤波');
subplot(2, 3, 6), imshow(filtered_img4), title('拉普拉斯算子锐化滤波');
请注意，这只是一个示例代码，具体的实现可能会根据你的需求而有所不同。