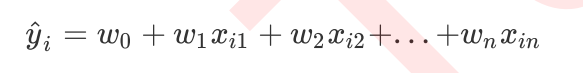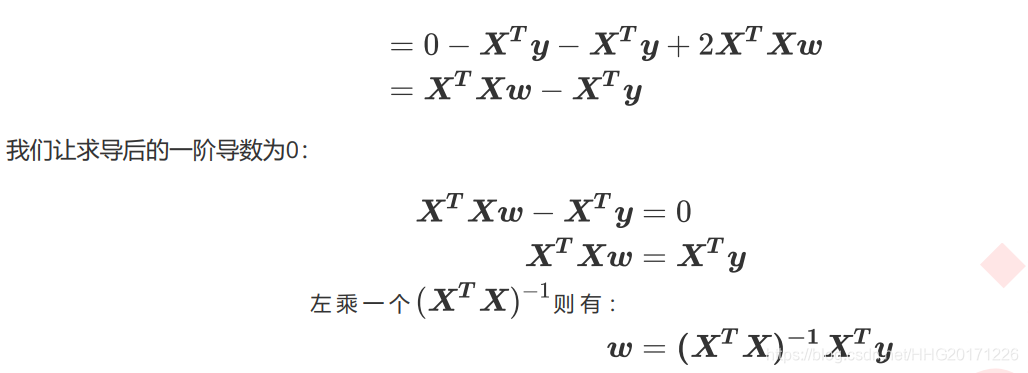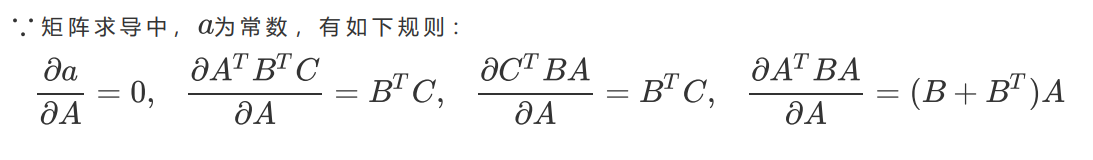到了这里，我们希望能够将 留在等式的左边，其他与特征矩阵有关的部分都放到等式的右边，如此就可以求出

使用普通最小二乘法的线性回归

class sklearn.linear_model.LinearRegression (fit_intercept=True, 
											normalize=False, 
											copy_X=True, 
											n_jobs=None
fit_intercept :布尔值，可不填，默认为True
 是否计算此模型的截距。如果设置为False，则不会计算截距
normalize:布尔值，可不填，默认为False
 当fit_intercept设置为False时，将忽略此参数。如果为True，则特征矩阵X在进入回归之前将会被减去均值（中心化）并除以L2范式（缩放）。如果你希望进行标准化，请在fit数据之前使用preprocessing模块中的标准化专用类StandardScaler
copy_X:布尔值，可不填，默认为True
 如果为真，将在X.copy()上进行操作，否则的话原本的特征矩阵X可能被线性回归影响并覆盖
n_jobs:整数或者None，可不填，默认为None
 用于计算的作业数。只在多标签的回归和数据量足够大的时候才生效。除非None在joblib.parallel_backend上下文中，否则None统一表示为1。如果输入 -1，则表示使用全部的CPU来进行计算。
 线性回归的类可能是我们目前为止学到的最简单的类，仅有四个参数就可以完成一个完整的算法。并且看得出，这些参数中并没有一个是必填的，更没有对我们的模型有不可替代作用的参数。这说明，线性回归的性能，往往取决于数据本身，而并非是我们的调参能力，线性回归也因此对数据有着很高的要求。幸运的是，现实中大部分连续型变量之间，都存在着或多或少的线性联系。所以线性回归虽然简单，却很强大。
 (sklearn中的线性回归可以处理多标签问题，只需要在fit的时候输入多维度标签就可以了。)
 代码：
 
#1. 导入需要的模块和库
from sklearn.linear_model import LinearRegression as LR
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import fetch_california_housing as fch #加利福尼亚房屋价值数据集
import pandas as pd
 #2. 导入数据，探索数据
housevalue = fch() #会需要下载，大家可以提前运行试试看
X = pd.DataFrame(housevalue.data) #放入DataFrame中便于查看
y = housevalue.target
print(X.shape)
X.columns = housevalue.feature_names
#3. 分训练集和测试集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
#重新建立索引
for i in [Xtrain, Xtest]:
    i.index = range(i.shape[0])
#如果希望进行数据标准化，还记得应该怎么做吗？
#先用训练集训练标准化的类，然后用训练好的类分别转化训练集和测试集
#4. 建模
reg = LR().fit(Xtrain, Ytrain)
yhat = reg.predict(Xtest)
#5. 探索建好的模型
#reg.coef_ 参数w1,w2.....wn
print(reg.coef_)
#截距  reg.intercept_
print(reg.intercept_)
                    回归分析整体逻辑回归分析（Regression Analysis）研究自变量与因变量之间关系形式的分析方法，它主要是通过建立因变量y与影响它的自变量 x_i(i=1,2,3… …)之间的回归模型，来预测因变量y的发展趋向。回归分析的分类线性回归分析- 简单线性回归- 多重线性回归非线性回归分析- 逻辑回归- 神经网络回归分析的步骤根据预测目标，确定自变量和因变量绘制散...
				
一、模型原理
Linear Rgegrssion基于最小二乘法的线性回归。是机器学习算法里面的基本算法，在sklearn.linear_model 的包里面。它能解决的问题是通过数据拟合，从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在。例如对于房价的预测。
二、线性回归的原理表示
我们先从最简单的函数看起，在只有一个变量的情况下，线性回归可以用方程：y = ax+b 表示。
Linear Regression模型会去不断的去调整下图直线的斜率和截距，使得残差平方和.
				
本文详细介绍使用SPSS软件进行多元线性回归的理论基础、操作步骤及结果分析。多元线性回归模型是指含有多个自变量的线性回归模型，用于解释因变量与其他多个自变量之间的线性关系。多元线性回归分析的基本步骤
(1)确定因变量与自变量，并初步设定多元线性回归方程。
(2)估计参数，确定估计多元线性回归方程。
(3)利用检验统计量对回归预测模型进行各项显著性检验。
(4)检验通过后，可利用回归模型进行预测，分析评价预测值。
`y=ax1+bx2+cx3+...+β`
线性方程来拟合某个规律.一元的时候是最小二乘法,高中的知识.多元的时候也是,暂时还没研究具体的公式和感受公式的含义.只当是高中公式一样,单纯往里套(调用sklearn的API)
2017年数模国赛B
主要目标是用红框的三个因素来拟合任务标价.先上代码.
from sklearn.linear_model import LinearRegression
import openpyxl
import matpl
要解决的是分析priceUSB与其他因素的关系，做出关系式，也就是Y为priceUSD，X分别为其他5个因素，做出多元线性回归方程。
①分析下每个因素和Y的关系（这一步就是只是看个开心而已其实）
def display_lr():
    pd_data=pd.read_csv('eth.csv')#原始数表
    #画出单因素...
				
波士顿房价预测是一个经典的线性回归问题。这个问题的目标是预测波士顿地区的房屋价格。为了解决这个问题，我们可以使用Python中的scikit-learn库。
首先，我们需要准备数据。在这个问题中，我们使用的是波士顿地区的房屋价格数据集。这个数据集包含了13个特征，包括了犯罪率、房屋所在位置的质量、交通是否便利以及房屋大小等因素。我们需要使用这些特征来预测房屋的价格。
接下来，我们可以使用scikit-learn中的线性回归模型来进行预测。线性回归模型通过拟合一个线性方程来预测因变量的值。在这个问题中，我们使用的是最小二乘法来拟合线性方程。
为了优化模型的准确度，我们可以使用交叉验证和正则化。通过交叉验证，我们可以评估模型在不同数据集上的表现，从而选择最佳的模型参数。正则化则可以限制模型的复杂度，从而防止过拟合。
最后，我们可以对模型进行评估。在这个问题中，我们使用均方误差（MSE）来评估模型的准确度。MSE越小，说明模型预测的准确度越高。
总之，通过使用scikit-learn中的线性回归模型，我们可以预测波士顿地区的房屋价格。这个问题不仅让我们熟悉了模型预测的基本流程，同时也拓展了我们在机器学习领域的知识。