协方差与相关系数

协方差(Covariance)定义为：

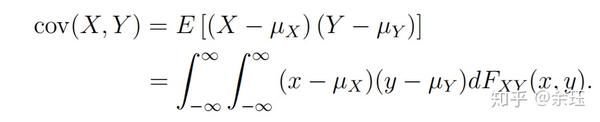
Cov（X,X）=Var（X）
协方差是对X与Y之间联动关系的一种测度，即测量X与Y的同步性。当X与Y同时出现较大值或者较小值时，COV>0,二者正相关。若X出现较大值时Y出现较小值，COV<0，二者负相关。该相关关系并不意味着因果关系

计算方式：

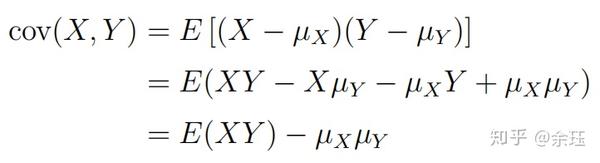
E为期望算子， \mu 为总体平均值。

从该式中我们可以发现，COV的大小与X、Y的大小有关。为了无量纲化，要对其进行标准化。就有了相关系数的概念。

相关系数定义为：

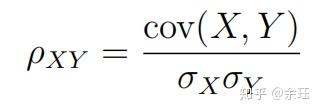
就是协方差除了XY各自的标准差，这样才能刻画XY之间联动性的强弱。

这里需要注意，相关系数应该叫 线性相关系数， 它只能反映出线性关系。

为何只能是线性关系的测度？

证明：

给出一个线性函数，Y=a+bX (b \ne0 ,X的方差存在）

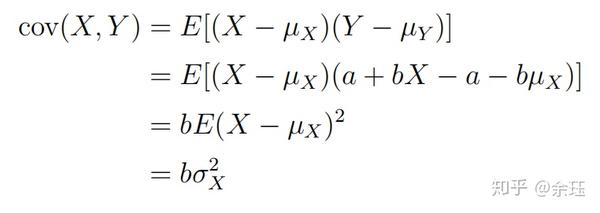
则，

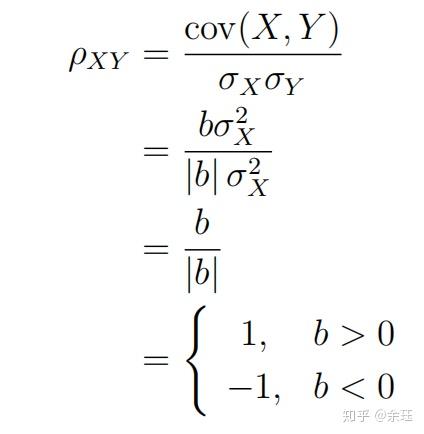
所以，当X与Y完全线性的时候，总有相关系数为1或者为-1.

扩展到一般线性模型：Y=a+bX+ \varepsilon

其中， \varepsilon满足E（\varepsilon）=0，var（\varepsilon）=\sigma^{2}

同理可证，

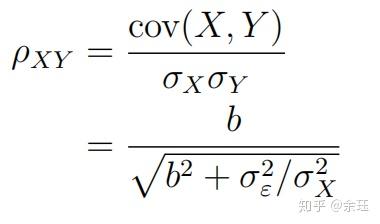
这里，相关系数与1之间的偏离程度就受 \sigma_{\varepsilon}^{2}/\sigma_{x}^{2} 的影响。

因此，其测度的只是一种线性关系，并且绝对值不会超过1。