LSTM-based Meta-Learning 随笔
本文总结了论文: Optimization as a Model for Few-Shot Learning
Few-Shot-Learning简介: 目前来说 Meta-Learning,one-shot-Learning,Few-Shot-Learning这几个词是等价的 ,Few-Shot-Learning的目标在于 从多个不同的学习任务(这些任务只包含少量训练样本)中,学习到一个模型,这个模型能够快速学习如何解决一个只含有少量训练样本的新任务 。
该论文提出了 一种基于LSTM的meta-learner模型 ,用于学习将会作用于另一个learner(比如一个具体任务的分类器)的最优化算法。 作者发现LSTM的更新规则和一般的梯度下降算法更新规则非常类似,因此将LSTM更新规则的输入替换为别的一系列参数(后面会详细讲到),用于更新Learner的 \theta 值。 需要先了解下LSTM的同学可以先移步此博客,个人觉得讲的很好:
1. 问题设置(Meta-Learning Problem Set-Up): 在一般的机器学习问题中,我们在数据集 D_{train} 中训练模型参数,在 D_{test} 中测试模型性能。在Meta-Learning问题设置下,我们处理的是Meta-sets \delta ,对其中每一个数据集 D\in\delta , D 划分为 D_{train} 和 D_{test} ,和一般的机器学习问题一样。同时, Meta-sets \delta 又被划分为多个Meta-sets \delta_{meta-train} , \delta_{meta-val} , \delta_{meta-test} ,如图1所示。我们的目标是在 \delta_{meta-train} 上训练一个“学习过程”,该过程输入一个 D_{train} ,输出一个学习器(classifer,learner),能够在对应的 D_{test} 上获得较高的效果。

2. 算法思路: 首先我们观察 一般的梯度下降算法(式1):
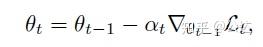
上述式子中, \theta 是learner的参数(非meta-learner), \alpha 是学习率,最后一项自然是梯度。
而在 LSTM中单元状态(cell state)的更新规则如下(式2):
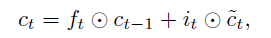
作者进行了如下的替换(式3,知乎上很多字符打不出来,因此就截图了,见谅):

在进行这样巧妙的替换之后,就能利用LSTM的状态更新公式,去更新learner的参数 \theta 了(只能说作者有一双善于发现的眼睛)。 Meta-Learner的目标,就是学习这个LSTM的更新规则,并将其应用于更新Learner的参数上。 作者随后定义了 i_{t} (输入门)以及 f_{t} (遗忘门),如式4,式5所示:


对于输入门参数 i_{t} ,它的作用相当于学习率 \alpha 。在此学习率是一个关于当前梯度;当前loss;当前参数 \theta_{t-1} 和上一轮的学习率 i_{t-1} 的函数。
对于遗忘门参数 f_{t} ,它代表着上一轮参数 \theta_{t-1} 所占的权重,在式3中只是简单地将其固定为1。但实际上1不一定是它的最优值,因为该值实际需要 根据当前learner是否是在一个局部最优值(bad local optima)并且需要大幅度更新以逃离该地区时 来判断,比如当loss很高,但是梯度却接近0的时候。因此它也有4项参数计算得来,同理于 i_{t} 。
作者还提到 该模型通过把学习单元初始状态的值 c_{0} 视为meta-learner的一个参数,也能对其进行学习, c_{0} 正对应于learner的参数初始值。 这样当来一个新任务时,meta-learner能给出一个较好的初始化值,从而进行快速学习。
3. 参数共享: 由于meta-learner是用于更新深度神经网络,因此learner通常会有成千上万个参数。为了避免meta-learner里参数数量爆炸,作者使用了参数共享,即在learner梯度的每一个coordinate(感觉翻译成坐标不是很准确,直接用英文了)上进行参数共享。 每一个coordinate都有自己的单元状态(cell state),但是所有coordinate在LSTM上的参数都是一样的。因此作者可以使用一个很小的LSTM模型,该模型对所有的coordinate更新规则是一样的。 作者在此基础上还进行了归一化的预处理,个人感觉比较麻烦,同时不重要,便不再赘述。 在此笔者认为每一个coordinate就相当于learner中的每一层,即对于相同一层的参数 \theta_{i} ,它们的更新规则是一样的,即 W_{I},b_{I},W_{F},b_{F} 是相同的(有不同见解请下方留言) 。
4. 训练过程: 在Meta-Learning中,训练的场景需要和测试时的场景一致, 即Meta-learner在训练集 D_{train} 上计算出一系列梯度,loss,learner的参数值,使用最后一步得到的learner的参数值在测试集 D_{test} 上测试。 过程如图2所示:

上图中,垂直的虚线左侧是在训练集 D_{train} 上进行训练,右侧则是测试集 D_{test} 上测试。 要注意的是:在训练集上训练时,Meta-Learner的参数是不会变的,最后使用在测试集上的loss对Meta-Learner的参数进行梯度下降的更新。
最后贴个算法伪代码,代码不难,需要讲解的之前已经都讲完了,具体如图3所示:

以上便是Optimization as a Model for Few-Shot Learning算法的核心思路以及流程,有不同的见解欢迎讨论。
写这么认真没人赞啊摔~

