环道同伦群(基本群)、k维同调群、纽结群的几何直观(张宏兵)

两空间拓扑同胚的必要条件是它们的紧致性相同，连通性相同，亏格相同，可定向性相同，欧拉示性数相同，环道同伦群(即基本群，用自由群)同构，k维同调群同构。纽结的同胚的必要条件还有纽结群同构，亚历山大多项式相同，手征相同等等。

这些都不一是充分条件，但作为必要条件也可以帮助我们区分是不是同胚空间。

环道同伦群(基本群)

环道同伦群也叫基本群，它的基础是空间内的环道分类。

如上图，基于一点p的环道，有一类叫1，任何1类或叫1伦的环道，可以连续缩为1点p。它们叫同伦的环道。从p出发，逆时针绕2圈回来，就表示为 1^2 ，顺时针绕3圈，可表示为 1^{-3} ， 最终等于没有动，所以是单位群员1。有的书上叫0伦(做为加法群的单位元)。

还有一类是要绕孔α，从基点p出发绕α孔跑n圈回到p，表示为 α^n ，逆时针绕则n为正整数，顺时针绕则n为负整数。绕α孔的环道都是同伦的。

还有一类是要绕孔β，从基点p出发绕β孔跑m圈回到p，表示为 β^m ，逆时针绕则m为正整数，顺时针绕则m为负整数，不绕不动则m就是0。绕β孔的环道也是同伦的。

等等。两环道同伦的较严格定义参见：

于是，绕α孔3圈，再绕β孔-2圈，再绕无孔6圈，再绕β孔1圈，可以表示为：

α^3·β^{-2}·1^6·β^1 ，

以诸如此类的式子(式子可以更简单也可以更复杂但是有限长度)表示群元素，就可以构成一个乘法群，叫环道同伦群，简称基本群。1, α, β等等就是群的生成元(1也可以不算生成元)。这些生成元之间没有关系，就是说不能由其它生成元算出(表示出)某一个生成元。

注意，下面两条环道是同伦的：

环道要基于基点，但环道同伦群的类型(有几个生成元，生成元之间的关系)，不依赖于p点的选择，选择另一点q为基点也一样，只要p与q可以道路连通。如下图，上半部分p与q点可以连通，选择哪一个作为基点，基本群一样，即不影响是同样的同伦型：

显然，球面的基本群是平凡群，只有一个生成元1，所有群元素都可以表示为 1^n ，其中n是整数，这也是一个平凡的无穷循环群。

k维同调群

1维同调群与环道同伦群类似(只是乘法群与加法群的区别，一般默认加法群符合交换律，是阿贝尔化的)，但是同调群可以是0维、1维、2维、3维等等的。

一个2维的环面，就是救生圈、轮胎面，其2维同调群就是1个0生成元，因为是2维闭合链，而且自身中只有一个类型的2维闭合链，就是它整体本身。其2维同调群的可以表示为n·0。其中n表示此2维链绕n圈，n是整数(包括正整数、负整数和0)。这是一个只有一个生成元的群，这个生成元就是单位生成元，所以是个平凡群，也是个无穷循环群，因为n是多少都会有 n·0=0.

2维环面上，有3类1维闭链(也就是闭曲线)：

0类的1维闭链，其独特特征是，可以分离出一块2维面。用刀在环面上沿0类闭链划一圈，可以割下一块面。1维的0类闭链，是它割下的这块二维面的1维边缘。之所以叫0类，是因为这类闭链可以同伦地缩为一个点，0对应的是同伦生成元1。

上图中，还有α类的1维闭链，其特征是不能使环面分离出一块面，但可以使环面断开。

上图中β类的1维闭链，只能使环面有个裂口。

α类与β类的闭链都不能缩为1点，因为它们有绕孔的特性。显示出环面有2个孔的拓扑学性质。

两个闭链何为同调？为什么说属于一个同调类？ 较准确的定义等一下给出。

环面的1维同调群中的元素，可以表示为诸如：

l·0 + n·α + m·β ， 等等。其中l, m, n等系数都是整数(包括正整数、负整数和0)

显然，只要把环面上的环道同伦群表示中的的整数指数变成为整数系数，再把乘法变成加法，把单位元1变成0，就成为1维同调群的表示了。换言之，环道同伦群的阿贝尔化之后，就会等价于1维同调群。(乘法一般认为没有交换律，而加法有交换律，于是加法群一般认为是阿贝尔的)

现在说说为什么α类的1维闭链(闭曲线)是同调的。因为，同属于α类的2条闭曲线，就可以从环面上分离出一个面。这两条α类的闭曲线，就是它们共同割下来的一个二维面(管状面)的1维边缘(即两个圆，可以用代表这两个圆的符号的减法表示)：

同样，两个β类的1维闭链，可以分割出一块二维面(二维的圆环形，类似两个同心圆及之间的面)，两闭曲线是此圆环面的边缘。所以，β类里的闭曲线都是1维同调的：

但是，α类的一条曲线，与β类的一条曲线，却不能导致分割出二维环面上的一块二维面出来。所以，它们不是同调的。

或者说，二维面上同调的两个一维闭曲线，可以通过连续移动互相重合，这种连续移动也是在二维面上进行的，或者说这种连续移动扫出了那一片二维面。

有相同结构的k维同调群，是两个拓扑空间同胚的必要条件。

0，α，β，等等，就是k维同调群的生成元。每个生成元可以乘以整数(整系数)，然后再相加，成为同调群的一个元素。这些生成元之间一般相互没有关系，是独立的生成元。

纽结群

良好的纽结可以如上图那样，投影到平面上，清楚看出交叉点，哪条线压另一条线。交叉点分出压线、被压线。相继的两条被压线段之间的一条线段，就可以看成是压线段，无论此处有没有真的压其它线段。如下图，粗线是压线段(不一定真的压线)，细线是被压线段：

可以给一个纽结的交叉点用数字编号，也可以给在交叉点压其它线的线用字母编号。

编号前可以先给纽结线一个行走方向：

纽结交叉点的一个显著特征是：手征性。

右手定则：

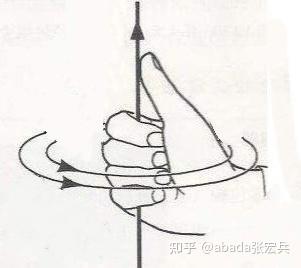
类似地，纽结的交叉点也可以分出是不是右手系的交叉点(右手叉)：

或左手叉：

(当然，有的作者对左右叉的定义与这里的刚好相反，这无关紧要。)

下面这个三瓣结，每个交叉点都是左旋的(这是三瓣结的特点，其它纽结的各交叉点的手征不一定一样)。即使我们给纽结线的走向重新定相反的方向，左旋的性质仍然不变：

下面这个三瓣结的每个交叉点都是右旋的：

对于每一个交叉点，读者可以盯住它及其邻近的压线段，设想从读者的某只眼睛为基点p，做绕各个压线段的环道。这需要把纽结看成三维空间中的虫孔隧道，而绕隧道的环道是三维空间中的环道。 下图中， x_k 表示此交叉点上的压线，简称“压线”， x_i 表示一个邻近的压线，它在此交叉点进入下行被压，简称“被压前”。 x_{i+1} 表示此交叉点被压出来之后的邻近压线，简称“被压后”。

我们把上空(读者眼睛处)p点引出的绕压线 x_k, x_i 和 x_{i+1} 的环道，也取名叫环道 x_k, x_i 和 x_{i+1} ，不至于混淆。

这些各交叉点的环道同伦群，就是纽结的纽结群。各交叉点的 x_k, x_i 和 x_{i+1} 与下述单位环道的代表元1，共同构成纽结群的生成元。

单位环道即1环道，是在各压线 x_k, x_i 和 x_{i+1} 下面绕一圈的环道，它实际上不绕任何纽结线(虫孔线)，从读者眼睛p点出发回到p点。

从上图可以看出，各生成元不是无关的，而是有关系的，对于右手叉，它们的关系表示在上图右下角的方框里。

下图是左手叉的纽结群的生成元的关系：

由于生成元之间存在关系，某些生成元可以用其它生成元表示出来，因此，给出最少需要的生成元，以及它们之间的运算关系，就决定了一个纽结群的群结构。

根据上面所述，纽结群的生成元的关系公式可总结如下：

---------------------------

右手叉：

(被压前)·(压线) = (压线)·(被压后)。

---------------------------

左手叉：

(被压后)·(压线) = (压线)·(被压前)。

---------------------------

注意，括号内都要应用压线段(即上行段)的字符编号。“被压前”，也是指临被压之前的压线字符编号。“被压后”，则是被压出来之后相继的压线段字符编号。

现在按上述公式计算如下三瓣结的纽结群表示：

显然，这是一个左手系的三瓣结，每个叉都是左手叉。 各叉编号为1，2，3。我们给纽结绳规定一个行走方向，如图。(规定相反的方向不影响下面的结论)。

我们再给各压线段(即上行段)编号： x_1, x_2, x_3 , 它们也是此纽结群的生成元的编号。群的单位生成元为1。

设 x_1=a，x_2=b ， 根据生成元的关系公式，可以计算出 x_3 用 a,b 表示出来的公式。

例如，根据1号【左手叉】及附近，有左手叉的关系公式：

(被压后)·(压线) = (压线)·(被压前)，即：

b·a = a·x_3 ，

上式两边左乘 a^{-1} ，得：

x_3 = a^{-1}ba .

于是有图：

再考察2处的左手叉及附近的生成元，有关系：

(a^{-1}ba) ·b = b·a ,

上式两边左乘 a ，得：

bab = aba .

这样，就把左手系三瓣结的纽结群的生成元减少为2个，即 a 和 b ，并且给出了它们的关系： aba = bab .

于是，左手系三瓣结的纽结群结构可以表示为：

G = {a,b|aba=bab} .

三瓣结的纽结群的三个生成元，与三维空间中XYZ笛卡尔坐标系分别绕X轴、Y轴、Z轴转动90°的操作，可以对应，群结构也同构。三瓣结与XYZ坐标系一样也有左右手系之分。参见：

正方结的纽结群表示：

如上图，把各个交叉点编号为1,2,3,4,5,6，把各压线段编号并同时用来表示纽结群的各生成元 x_1,x_2,x_3,x_4,x_5,x_6 .

设压线段(也是生成元)：

x_1=a, ~\\ x_2=b,~\\ x_3=c,

然后可以用 a,b,c 把其它压线段(生成元)也表示出来：

首先注意1号交叉点，是个【右手叉】，适用右手叉关系公式：

(被压前)·(压)=(压)·(被压后)，此1号交叉处即：

a·b=b·x_4 ,

上式两边左乘 b^{-1} , 得：

x_4=b^{-1}ab .

再看2号交叉点，是个【左手叉】，适用公式：

(被压后)·(压)=(压)·(被压前)，即： a·c=c·x_5 , 两边左乘 c^{-1} , 得：

x_5=c^{-1}ac .

再看3号交叉点，是右手叉，按关系公式有： b·x_4=x_4·x_6 , 把刚才已经得到的 x_4=b^{-1}ab 带入，可得：

x_6=b^{-1}a^{-1}bab .

于是，图可以标注为：

再继续观察第5号交叉点，是右手叉，利用公式有：

(b^{-1}ab)·(b^{-1}a^{-1}bab)=(b^{-1}a^{-1}bab)·b ,

化简，可得关系：

aba=bab .

最后看4号交叉点，左手叉，用关系公式有：

c·(c^{-1}ac)=(c^{-1}ac)·(b^{-1}a^{-1}bab) ,

把前面已得关系 bab=aba 先代入上式，再化简，可得：

cac=aca .

于是，正方结的纽结群可以表示为：

{ a,b,c \space | aba=bab, aca=cac }.

从群结构看，正方结是2个三瓣结的合成，从图形上直观看，的确也是左边的一个左手系的三瓣结与右边的一个右手系的三瓣结的合成。

(续：

)

_______________________

参考文献：

1，Armstrong：《基础拓扑学》

2，Wikipedia： Knot Theory 等词条。

并引用了上述文献中的某些图片。