【群论入门】(1):起源与应用
解方程给数学和科学带来深远影响远超其自身,但直到19世纪,代数基本等同于解方程,以至于今天, 代数基本定理 (下面将提及)竟然“荒唐”地认为不属于代数,基本定理竟然被开除,简直骇人听闻!那是由于它是关于方程的定理,诞生于代数与方程是同义词的时代。
解方程的里程碑:
- 公元前2000年,古巴比伦人在一元一次方程时产生了分数,即有理数;
- 数百年后,他们已了解了二次方程的根式解,产生了无理数;
- 16世纪,意大利数学家Cardano和Bombelli在求解一元三次方程时发明了 虚数 。著名数学家Sir Michael Atiyah(1929-2019)爵士说, \sqrt{-1}=i 是数学史最伟大的单个发明;
- 探索高于4次的多项式方程是否存在求根公式,催生了 群论 。
- 求解线性方程组孕育了 线性代数 ;
也因此,复数和线代都与群论内部结构相同,联系紧密。
群论的诞生是代数、几何和数论三个领域的发展共同推动的。
1800年左右, 人们已经会解1至4次方程 ,但对于求解更高的次的方程还没有头。为了回答这个问题,挪威数学家阿贝尔(Niels Henrik Abel,1802-1829)的贡献良多,其中最著名的是首先证明了5次方程没有求根公式。另外, 拉格朗日 做了非常重要的总结性工作和提出了新的思想,可以说是万事俱备只欠东风。

法国数学家伽罗瓦(Évariste Galois,1811-1832)进行群论的开创性工作。 代数基本定理 告诉我们:方程是几次方就对应几个根,群论提供一种证明代数基本定理的方法。

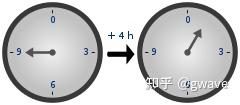
差不多同时(1798),高斯(Carl Friedrich Gauss, 1777-1855)在其经典的 数论 著作中提出了 模算术 (Modular Arithmetic),其逻辑也与 群 一致。下图中,时钟的模数为12, 9+4=13\equiv1 。
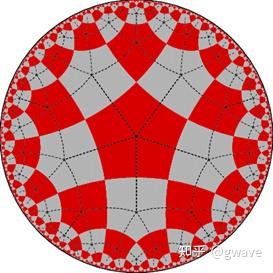
1800年代,已统治了两千年的欧几里得几何面临革命, 双曲几何 和 球面几何 等非欧几何呼之欲出。人们很快发现 群 是研究这些几何的重要工具,1827年,莫比乌斯(August Ferdinand Möbius, 1790-1868)在完全不了解群的概念的情况下,使用特定群的几何不变性这一事实对几何图形进行分类。
环 的概念是在证明 费马大定理 过程中产生的,数论中的整数集合是一个环,与几何、高次方程求解一样, 数论 为抽象代数的发展提供了实例和源泉。
于是,“ 群 ”的概念被从不同领域中被抽象出来,并演化出 环 、 场 、 Modules 和 向量空间 等概念。这些概念,今天统称为 抽象代数 ,也称 近世代数 (Morden Algebra)。你要是和一群搞数学的人在一起,他们就称之为“代数”,但你可能发现他们聊的内容的与你印象中的代数完全不同!
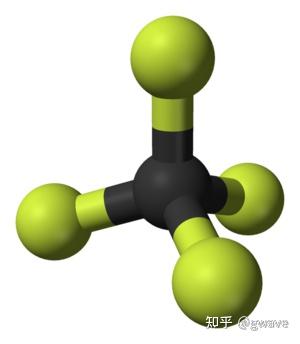
群不仅已经深入到几乎所有的数学分支,也被广泛应用于物理、化学和计算机等领域。上图中的 CCl_4 分子具有四面体形状,其对称组有24个元素,化学家使用对称基团对分子进行分类,并预测其化学性质。李群是量子力学的重要工具,在机器人领域,李群被应用于刚体位移群的矩阵表示。也有人尝试用群论来解释深度学习是如何工作的。 [1]

除了基础的 集合 概念,说起来学习 群论好像 不需要什么数学基础,为了能轻松而牢固地理解 群 的概念,下一篇文章将通过具体的例子来解释群的特点,请戳➡️ 这里 !
本系列旨在提供一个人人都能理解的群论入门,但又不失数学的严谨性,仅要求初中以上数学,和具有数学思维(证明、集合、抽象等)。
延伸阅读: