有关基本图论定义与术语的知识老是记不清楚,这里做一个归纳:
图与网络(Graph and Network):
二元组(V,E)
称为
图(graph)
。V为
结点(node)
或
顶点(vertex)集
。E为V中结点之间的边的集合。
点对(u,v)
称为
边(edge)
或称
弧(arc)
,其中u,v属于V,称u,v是
相邻的(adjacent)
,称u,v,与边(u,v)相关联(incident) 或相邻。
若边的点对(u,v)有序则称为
有向(directed)边
,其中u为
头(head)
,v称为
尾(tail)
,所形成的图称为
有向图(directedgraph)
,意即--对于u来说,(u,v)是
出边(outgoing arc)
,对于v来说,(u,v)为
入边(incoming arc)
,反之,若边的点对无序则称为
无向(undirected )边,
所形成的图称为
无向图(undirected graph).
若图的边有一个
权值(weight)
,则称为
赋权边
,所形成的图称为
赋权图(weighted graph)
或
网络(network)
,用三元组G(V,|E,W)表示网络,其中W表示权集
它的元素与边集E--对应,在流网络中(flow network),权集W友记作C,表示
容量(capacity)
。
图的术语(Glossary of Graph):
简单图(simp graph)
: 没有环,且没有多重弧的图称作简单图。
领域(neighborhood )
:在图中与u相邻的点的集合{v|v属于V,(u,v)属于E},称为u的领域,记为N(u)。
度(degree )
一个顶点的度是指与该边相关联的边的条数,顶点v的度记作deg(v)或d.
握手定理:无向图:
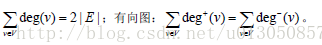 。
。
入度(indegree )
:在有向图中,一个顶点v的入度是指与该条边相关联的入边(即边的尾是v)的条数,记作deg+(v)。
出度(outdegree)
:在有向图中,一个顶点v的入度是指与该条边相关联的出边(即边的头是V)的条数,记作deg-(v)。
孤立点(isolated vertex)
:度为0 的点。
叶(leaf)
:度为1 的点。
源点(source )
:有向图中,deg+(v)=0的点。
汇点(sink)
:有向图中,deg-(v)=0的点。
子图(sub-graph)
: G'称作图G的子图:

点导出子图(induced subgraph)
: 设V∝V(G),已V'为顶点集,以两段点均在V‘中的全体边为边集所组成的子图,称为G的有顶点集V’导出的子图,简称为点导出子图,称为G[V']。
点集的补集
:记
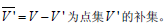
特殊的图:
零图
(null graph)
:
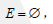 即只有孤立点的图,n阶零图记为Nn。
即只有孤立点的图,n阶零图记为Nn。
二分图
(bipartite graph)
:若图G的顶点集可以划分两个非空子集X和Y,即V=X∪Y且X∩Y=空集,且每一条边都有一个顶点在X中,而另一个顶点在Y中,那么这样的图称为二分图。
#A氪金带东
实验室里原先有一台电脑(编号为1),最近氪金带师咕咕东又为实验室购置了N-1台电脑,编号为2到N。每台电脑都用网线连接到一台先前安装的电脑上。但是咕咕东担心网速太慢,他希望知道第i台电脑到其他电脑的最大网线长度,但是可怜的咕咕东在不久前刚刚遭受了宇宙射线的降智打击,请你帮帮他。
提示: 样例输入对应这个图,从这个图中你可以看出,距离1号电脑最远的电脑是4号电脑,他们之间的距离是3。 4号电脑与5号电脑都是距离2号电脑最远的
点
,故其答案是2。5号电脑距离3号电脑最远,故对于
图(
Graph
)是一个用于描述一组对象之间关系的数学结构。这些对象被称为顶
点
(Vertex),也称为节
点
(Node)或
点
(Point),而对象之间的关系则通过边(Edge)来表示,边也称为链接(Link)或线(Line)。图通常以图解形式描绘为顶
点
的一组
点
或环,并通过边的线或曲线连接。
这篇文章首先发在bilibili。
计划读这本Modern
graph
theory, Bollobas (GTM184)。每天会发一部分提纲。今天的部分是1.1.1节
definition
s。有过
图论
基础的朋友应该
基本
都知道,那我们的叙述就尽量简单但覆盖全面一
点
。
1.
基本
定义
(下汉语
术语
都由笔者捏造。在使用时将使用
英文
)
图(
graph
)、顶
点
(vertice)、边(edge)、连接(join)、相邻(neighbouring)、由…产生(be incident with)、
子图
(subg
边
导出
子图
:选出若干条边,以及这些边所连接的所有顶
点
组成的图称为 边
导出
子图
。
点
导出
子图
:选出若干个
点
,以及两端都在该
点
集的所有边组成的图称为
点
导出
子图
。闭合
子图
:
定义
在有向图上。
点
集 V
导出
的 闭合
子图
是所有 V可达的
点
的
点
导出
子图
。其精确
定义
为若 x在
子图
内,则 x的所有出
点
和出边均在
子图
内的原图
子图
;等价于每个
点
能到的所有
点
都在
子图
中。差分约束问题为给出若干形如 xa−xb≤c或 xa−xb≥c的不等式,求任意一组 x的解。我们发现,只要 xa,xb。
先建图,连接有向边(i,a[i]) 若邀请x 则要邀请以x为起
点
遍历的联通分量.
因为每个
点
只有一个出边. 所以每个联通分量都是以 一个环 + 若干个分支(tributary)组成.
选择该联通分量任意一
点
都要把环选上 ,...
建立了图(
graph
)的认识,“树”就好理解了。“树”是一种很特别的图(
graph
)。用图来
定义
“树”:任意2
点
之间都连通,并且没有“环”的图。下面的图就是一颗树,因此,树是图的特例。
图论
相关
定义
一个图(
graph
) G = (V, E) 由顶
点
(vertex)的集合 V 和 边(edge)的集合E组成,有时也把边称作弧(arc)。如果图中的边是带方向的,那么图就是有向图(directed),否则就是无向图。如果有一条边从顶
点
v到顶
点
w,则称顶
点
v和w邻接(adjacent)。如果图中有一条从一个顶
点
到它自身的边,那么图是带环的,无向图中的环意义不大(无向图中很容易出现还),...
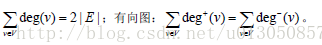 。
。

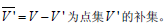
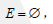 即只有孤立点的图,n阶零图记为Nn。
即只有孤立点的图,n阶零图记为Nn。