X ~ 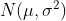：随机变量X的取值 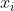和其对应的概率值P(X = 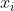) 满足正态分布（高斯函数）

• 很多 随机现象 可以用正态分布描述或者近似描述
• 某些 概率分布 可以用正态分布近似计算

1.概率密度函数：

2.正态分布函数曲线的性质：

3.正态分布的概率分布函数

概率分布函数是正态分布曲线的定积分，公式为：

正态分布曲线与x轴围成的面积是1(积分区间是负无穷到正无穷)

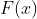的值代表P(X <=  x)

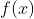的值代表P(X = x)

正态分布 （Normal distribution）又成为 高斯 分布（Gaussian distribution） 若随机变量X服从一个数学期望为、标准方差为的 高斯 分布，记为： 则其概率密度 函数 为： 正态分布 的期望值决定了其位置，其标准差决定了分布的幅度。因其曲线呈钟形，因此人们又经常称之为钟形曲线。我们通常所说的标准 正态分布 是的 正态分布 ： 概率密度 函数 首先，我们来介绍一下什么是 正态分布 ？ 正态分布 的图形如下，符合 正态分布 的数值有以下几个特点：1.数值中的平均值所对应的位置是最高点；2. 正态分布 曲线，以平均数为中心点，左右对称。3. 正 态曲线从中心点开始，向两侧逐渐均匀下降。那么，我们如何在excel中使用 正态分布 函数 呢。首先来看一下我们的公式定义：返回指定标准值和方差的 正 态累积分布 函数 值=N... 参考博客：https://www.cnblogs.com/htj10/p/8621771.html概率密度 函数 的意义：理解概率密度 函数 - 知乎 (zhihu.com)若随机变量 服从一个位置参数为、尺度参数为的概率分布，且其概率密度 函数 为:：是 正态分布 的位置参数，描述 正态分布 的集中趋势位置。概率规律为取与邻近的值的概率大，而取离越远的值的概率越小。 正态分布 以为对称轴，左右完全对称。 正态分布 的期望、均数、中位数、众数相同，均等于。 位置（形状）参数控制分布 函数 形状的变化。：是 正态分布 的尺度参数，描述 正态分布 若随机变量X服从一个数学期望为μ、标准方差为σ2σ^2σ2的 高斯 分布，记为：X∼N(μ,σ2σ^2σ2)。         其概率密度 函数 为： f(x)=1σ2πe−(x−μ)22σ2,−∞<x<∞ f(x... f(x)=12π−−√σe−(x−μ)22σ2f(x)=12πσe−(x−μ)22σ2 则这个随机变量就称为 正 态随机变量， 正 态随机变量服从的分布就称为 正态分布 ，记作X∼N(μ,σ2)X∼N(μ,σ2)。 当μ=0,σ=1μ=0,σ=1时，称为标准 正态分布 。X∼N(0,1)X∼N(0,1) f(x)=12π−−√e−x22f(x)=12πe−x22 如下图是一般... 1）集中性：曲线的最高峰位于 正 中央，且位置为均数所在的位置。 2）对称性： 正态分布 曲线以均数所在的位置为中心左右对称且曲线两段无线趋近于横轴。 3）均匀变动性： 正态分布 曲线以均数所在的位置为中心均匀向左右两侧下降。 4）曲线与横轴间的面积总等于1。 正态分布 函数 公式如下： 公式解释：其中μ为均数，σ为标准差。μ决定了... 若随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布，且其概率密度 函数 为 f(x)=12π−−√σe−(x−μ)22σ2f(x)=12πσe−(x−μ)22σ2f(x)=\frac{1}{\sqrt{2π} \sigma}e^{-\frac{(x- \mu)^{2}}{2 \sigma ^{2}}} 则这个随机变量就称为 正 态随机变量， 正 态随机变量服从的分布就称为 正 ... 最近在整理数据时，忽然想到数理统计的其中一种分布，相信作为质量人一定不陌生，我们常常提到数据的分布是否服从 正态分布 ，这是对一组连续数据分布一种描述，还会涉及到如何检验 正态分布 ，对于这个分布的来龙去脉和数学分解，小编今天在这篇小文中就不罗嗦了，期望后续在学习时分享笔记，一起探讨数理统计和实践结合的案子及其个人理解。 今天就着重分享在已知分布 函数 的U(X)如何在标准 正态分布 ...