3 个回答
一元三次方程,永远都是三个根。
分两种情况,1,三个都是实根;2,两个虚根一个实根。
没有第三种情况,譬如什么三个虚根或一虚两实之类。
其中第2种情况,两个虚根必然互为共轭。(正因为这个原因,所以不存在“三个虚根“或“一虚两实”这类情况)
第1种情况,又分为三个不等的实根(无重根),两重根,三重根,这三种情况 。
如果要判断具体属于哪种情况,也一样有判据。但这个判据很复杂,先要将方程化为“缺二次方项”型,然后再用判据展开判断,这个判据涉及及求根公式。这一套程序走下来,要花很多时间。
所以,不如你准备一个手机上或电脑上那种具备函数绘图功能的计算器,画出方程左面那个函数的图像,然后观察一下函数图像与x轴有几个交点。大体上你就可以判断出:
一、函数与x轴有三个交点,这属于“无重根”,或“三个不同实根”。
二、函数与x轴有两个交点,这属于“两重根”,其中有一个交点是切点,这就是重根的位置,另一个交点则是第三根。
三、函数与x轴有一个交点,这属于“三重根”或“一实两虚”。区别是要看这个交点是否是拐点(同时也相切),若是,则属于三重根;若否,则属于“一实两虚”。虚根在图面上是不显示的。
当然,由于绘画都是有一定范围的,有时候显示不完整,故这方法有局限性,不一定全都好用,但“大体上”还是能用的。
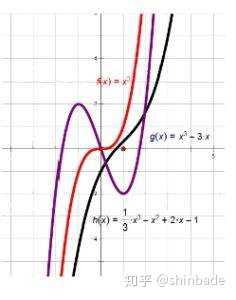
下图就是第一和第三种情况的典型图示。红线属于“三重根”,黑线属于“一实两虚”,紫线属于“三实根”。
如果把紫色线条朝上平移(或朝下),到达与x轴相切的位置,那就属于“两重根”的情况,其中切点是重根,另一个交点是第三根。
当然,如果你会微积分,也可以通过研究其导数,来大体上明确曲线的形状。不一定非得用计算器作图。对应的结论是:
无极值(即导数永不为0),是黑线的情况; 一实两虚
只有一个点,其导数为0,二阶导数也为0,这个叫作拐点,且拐点在x轴上,这是红线的情况; 三重根。
有两个极值点(即一阶导数为0的点),且一正一负,是紫线的情况; 无重根(三实根)。
有两个极值点,但其中有一个在x轴上,那就属于图中没画出的情况(即,紫线向上平移或向下平移的情况)。 两重根 。
哇啊!被这种不知道多少年的老问题找上了啊!!fukoudesi!
啊没有。开个玩笑。
先放答案(纯手算,赏个赞呗):

我是真不相信这种常识性问题居然在知乎还存在缺口,于是我找了一下,发现已经有名为“三次多项式的判别式是什么?”的问题了:
然而里面只有两个回答(就像此时此刻的这个回答一样)。
(就在刚刚,第三个回答出现了)
想了想,我觉得还是有必要稍微补充和解释一下一元三次方程的求解思路。
首先第一点,也是求解三次方程时常做的第一步,通过左右平移和尺缩解决三次和二次的系数。更直白来说,就是把
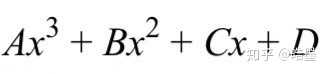
变成
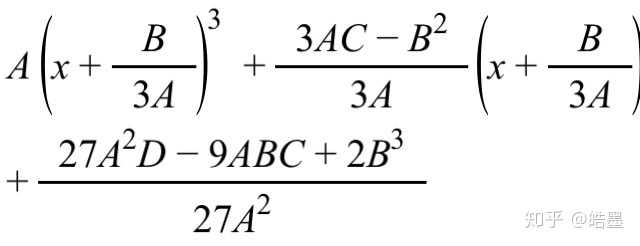
令t=x+B/3A,并令图中一次项与常系数分别为B’,C’,则只要解决形如Ax^3+B’x+C’=0的问题就可以了(容易证明,这两种形式是可以互化的且解数完全一样)。
我们只需考虑更一般的三次方程:
X^3+aX=b.
求导即知当a≧0时方程恒为一解(利用单调性同样易证),当a<0时,利用导数计算其极值后边界式为
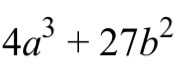
记为delta.
则delta>0时,方程恰有一实数解;
delta=0时,方程恰有两实数解,包含双重根;
delta<0时,方程有三个实数解。
回溯推理过程,有
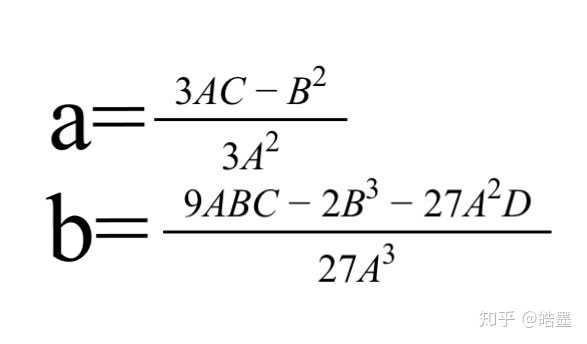
故3AC≧B^2时仅有一解其余情形delta为(约去了729A^6):
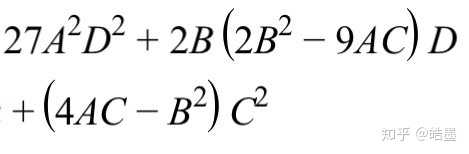
如果保留二次方程中delta>0时有全解的习惯,我们将delta取负数,再将大写字母换成小写(鬼知道我开始为什么要打大写),就变成
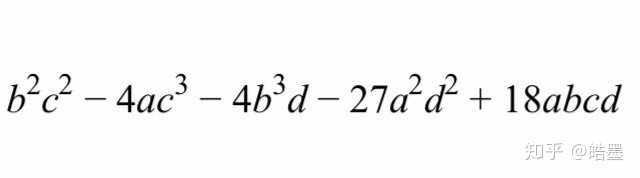
这与[匿名用户](我不知道是谁啦,反正就是2018-11-02的回答)在问题 三次多项式的判别式是什么? 中给出的答案相一致(没有算错,啊,太好了)。
另外对于提到过的3ac≧b^2的情况,这时delta可视为以d为主元开口向下的二次函数(如图6所示),其判别式为16(b^3-3ac)^3,这表明3ac≧b^2时delta≦0,即delta的判断在3ac≧b^2时也是准确的,故其可作为可靠的判别式而不需考虑其它关系。
结语:对于一元三次方程:
ax^3+bx^2+cx+d=0,
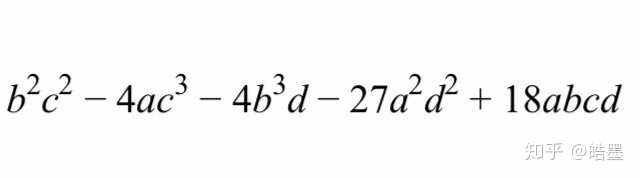
记为delta,为其(实数)根的判别式。
其中,delta>0时,方程恰有一实数解;
delta<0时,方程有三个实数解。
特别地,delta=0时,需检查计算b^2-3ac的值,若其为0,则恰有一根,若其为正,则恰有两根(可证明此时其值非负)。
也即:

至此讨论是结束了。
手算不易,给个赞呗!

