固体物理笔记(6)：电荷密度波

本章我们讨论一种特殊的费米液体面的不稳定性：一种自发形成的静态 电荷密度波（charge density wave， CDW） 。这一现象和晶格结构的周期是不相称的，经常出现在一些准一维的的金属中。CDW和自旋密度波(spin density wave)在高温铜氧化合物超导化合物中以 条带（stripes） 中呈现，并且和超导形成直接的机制竞争。

CDW的主要特点可以总结如下：

• 导带电子的密度呈现空间调制，这一现象可以直接通过 扫描隧穿显微镜（Scanning Tunnel Microscopy, STM） 观察到
• 电荷分布的密度的周期通常对应于一个费米面的叠套矢量(nesting vector)
• 被CDW作用的晶格结构也会被周期性的调节，这一变化可以通过 X-ray，电子和中子散射观察到，或者是 扫描探针 (Scanning Probe)技术
• CDW通常伴随着声子耗散曲线畸变（anomalies/wiggles）的增加，对应于CDW相变的晶格扭曲的声子能量会被减少甚至是在相变的时候会到零。
• 费米面附近的状态密度会在CDW相变的时候减少，这可能会导致电阻的降低，热传导率的降低，反射率的降低，Pauli顺磁相的降低，以及异常的 Seebeck系数或者霍尔效应。
• 状态密度的减少是由于一个局部的或者是一个完整的费米面间隙。间隙可以通过隧穿、光发射、红外吸收/反射以及正电子湮没实验测量出。
• 虽然状态密度会减少，但在带隙上下的状态密度会大幅增加，可以通过光发射以及隧穿实验测出。

晶格电子相互作用

由于电子和晶格上的离子都是带电的，一个CDW相主要是两件事：一个被调节的电子密度以及一个被调节的晶格结构。在研究CDW的时候我们必须考虑电子-声子相互作用。这些相互作用会影响材料的磁化率以及晶格的刚性 （弹性敏感性，elastic susceptibility） 。

晶格的弹性敏感性

考虑一个简单的Bravais晶格，平衡位置为 \bold{R}_j ，如果晶格被轻微的畸变，原子的位置会发生移位 \bold{r}_j = \bold{R}_j + \bold{u}_j ，我们加一个周期性的力场

\bold{F}_j = \bold{F} \exp{(i\bold{q}\bold{R}_j)} + c.c.

该力场会施加一个周期性的扭转

\bold{u}_j = \bold{u} \exp{(i\bold{q}\bold{R}_j)}+c.c.

我们可以定义晶格的敏感性

\bold{u} = \chi_{lat}(\bold{q})\bold{F}

这对于我们计算晶格扭曲产生的弹性能量有用。我们可以通过施加一个缓变的周期性调节的外力，

\bold{F}(x) = x \bold{F} = \frac{x\bold{u}}{\chi_{lat}(\bold{q})}

这个外力产生的扭曲会有一个幅度

\bold{u}(x) = x \bold{u}

由此做的功为

\mathrm{d}W = \frac{N}{V}\int \mathrm{d}\bold{r}\mathrm{d}x\bold{F}(\bold{r},x)\bold{u}(\bold{r},x) = x\mathrm{d}x \frac{1}{\chi_{lat}(\bold{q})}\frac{N}{V}\int \mathrm{d}\bold{r} \bold{u}^2(\bold{r})= 2x \mathrm{d}x N \frac{1}{\chi_{lat}(\bold{q})}|\bold{u}|^2

上面 N 是系统内的粒子数量，我们将求和换成积分，最后我们有

E_{lat} = 2N\frac{1}{\chi_{lat}(\bold{q})}|\bold{u}|^2\int_0^1 x\mathrm{d}x = N \frac{1}{\chi_{lat}(\bold{q})}|\bold{u}|^2

晶格畸变对电子的影响

我们设 \tilde{U}(\bold{r}) 为一个离子产生的静电场（考虑屏蔽后的），在晶格畸变后总的势场为

\begin{align*} \phi(\bold{r}) &= \sum_{i}\tilde{U}(\bold{r}_i - \bold{r}) - \tilde{U}(\bold{R}_i - \bold{r}) \\ &= \sum_i \bold{u}_i \nabla \tilde{U}(\bold{R}_i - \bold{r}) \\ &= \frac{1}{V_0}\int \mathrm{d} \bold{r}' \bold{u}(\bold{r}')\nabla\tilde{U}(\bold{r}'-\bold{r}) \end{align*}

其中 V_0 是单胞的面积，最后的一个积分通过分部积分

\int \mathrm{d} \bold{r}' \bold{u}(\bold{r}')\nabla\tilde{U}(\bold{r}'-\bold{r}) = \oint \tilde{U}(\bold{r}'-\bold{r})\bold{u}(\bold{r}') \mathrm{d}\bold{s} - \int\mathrm{d}\bold{r'} \tilde{U}(\bold{r}'-\bold{r})\nabla \bold{u}(\bold{r}') = -i(\bold{q}\bold{u})\tilde{U}_{\bold{q}} \exp{(i\bold{q}\bold{r})}+c.c.

在上式推导过程中我们忽略环积分因为形变 \bold{u} 是周期性变化的，最左端的 \tilde{U}_{\bold{q}} 是势场的傅里叶分量。势场是周期性的并且有幅度

\phi = -i (\bold{q}\bold{u}) \tilde{U}_\bold{q}

该势场产生一个周期性调节的电荷分布

\rho_{el} = \chi(\bold{q})\phi = -i(\bold{q}\bold{u})\tilde{U}_{\bold{q}}\chi(\bold{q})

电子对晶格刚性的影响

为了计算电子对晶格刚性的影响，我们需要计算由于电荷分布变化引起的静电势能。

\mathrm{d}W_{el} = \int \mathrm{d}\bold{r}\phi(\bold{r},x) \mathrm{d}\rho_{el}(\bold{r},x) = 2x \mathrm{d}x (\bold{q}\bold{\hat{u}})^2 |\tilde U_{\bold q}|^2\chi(\bold{q}) V

总的静电势能为

E_{el} = 2|\bold q\bold u|^2 |\tilde U_q|^2 \chi(\bold{q}) V \int_0^1 x \mathrm{d}x = |\bold q\bold u|^2 |\tilde U_{\bold q}|^2 \chi(\bold{q}) V

加上上面计算的晶格储存的弹性势能

E_{total} = E_{lat} + E_{el} = N|u|^2\bigg[\frac{1}{\chi^{(0)}_{lat}(\bold{q})}+(\bold{q}\hat{\bold{u}})^2\frac{V}{N}|\tilde{U}_{\bold{q}}|^2 \chi(\bold{q})\bigg]

其中 \chi^{(0)}_{lat}(\bold{q}) 是在无电子晶格相互作用时候的晶格敏感性。从上式中我们可以得到一个新的 E 和 |u|^2 的关系式，即一个新的晶格敏感性，该敏感性考虑到了电子和晶格的相互作用

\chi_{lat}(\bold{q}) = \frac{\chi_{lat}^{(0)}(\bold{q})}{1+2\tilde{\lambda}_{\bold{q}}\frac{\chi(\bold{q})}{e^2\nu(\varepsilon_F)}}

上式中wo们引入了一个无量纲的电子晶格相互作用屏蔽常数

\tilde{\lambda}_{\bold{q}} = \frac{e^2}{2}(\bold{q}\cdot\hat{u})^2|\tilde{U}_\bold{q}|^2V_0 \nu(\varepsilon_F)\chi_{lat}^{(0)}(\bold{q})

其中 V_0 = V/N 是单元晶胞体积。主要到新的敏感性总是被最初的高，这是因为电子的磁化率是负的。倒带电子会即使运动去填补由于晶格扭曲造成的电荷分布不均，因此最后让晶格更加软。

另外一个重要的点在于，上述原理只适用于纵向的晶格扭曲，即那些造成离子晶格和离子电荷密度波压缩的震动。因此，该震动对应的矢量 (\bold{q}\hat{\bold{u}}) 不应该垂直于密度波的前进波矢。

声子频率和晶格刚性

弹性的敏感性实际上在实验中是可以测出来的， 因为其直接和声子的频率相关联 。后者可以通过非弹性的中子或者光散射测出。

对应于波矢为 \bold{q} 的声子离子的位移可以写作

\bold{u}_j(t) = \bold{u}\exp{(i[\bold{q}\bold{R}_j - \omega_\bold{q}t])}+c.c.

反作用力为

\bold{F}_j(t) = M\ddot{\bold u}_j(t) = -\omega^2 M \bold{u} \exp{(i[\bold{q}\bold{R}_j - \omega_\bold{q}t])}+c.c.

其中 M 为离子的质量。

另一方面，根据晶格敏感型的定义，反作用力为

\bold{F}_j(t) = -\frac{1}{\chi_{lat}(\bold{q})}\bold{u}\exp{(i[\bold{q}\bold{R}_j -\omega_{\bold{q}}t])}+c.c.

因此我们有

\frac{1}{\chi_{lat}(\bold{q})} = M\omega_{\bold{q}}^2

电子对声子频率的影响

我们回到前面的式子

\chi_{lat}(\bold{q}) = \frac{\chi_{lat}^{(0)}(\bold{q})}{1+2\tilde{\lambda}_{\bold{q}}\frac{\chi(\bold{q})}{e^2\nu(\varepsilon_F)}}

结合晶格敏感性和声子频率的关系，该式给出了一个全新的意义，即一个重整化后的声子频率

\Omega_{\bold{q}}^2 = \omega_{\bold{q}}^2 \bigg[1+2\tilde{\lambda}_{\bold{q}}\frac{\chi(\bold{q})}{e^2\nu(\varepsilon_F)}\bigg]

耦合常数可以重新写作

\tilde{\lambda}_{\bold{q}} = \frac{e^2}{2M\omega_{\bold{q}}^{(0)}}(\bold{q}\cdot\hat{u})^2|\tilde{U}_\bold{q}|^2V_0 \nu(\varepsilon_F)

由于敏感性依赖于 q ，重整化后的声子频率在某些特定波矢 q 会特别显著，即很强的nesting。这样在声子耗散谱上造成的凸起我们称之为 科恩反常（Kohn anomalies，硬翻的…） 他们通常依赖于温度。

另外在上述讨论中还存在一个问题，即 \bold{F}_j(t) = -\frac{1}{\chi_{lat}(\bold{q})}\bold{u}\exp{(i[\bold{q}\bold{R}_j -\omega_{\bold{q}}t])}+c.c. 的一个假设条件在于晶格的敏感性并不依赖于频率。因此我们的上述当只有当电子的运动速度远远快于声子的震动速度才成立，此时电子可以非常快速的弥补声子震动造成的电荷分布不均匀。这一假设也被称作 绝热近似（adiabatic approximation） ，实际应用起来该假设基本上都是成立的，主要因为电子比离子的质量要轻很多。

CDW相变

上述的所有讨论都是为了给出一个现象，即电子因为费米面nesting的影响并不一定会影响整体的费米气体的稳定性，但却有可能让晶格变软，从而形成周期性的晶格波动。特别的是，

\chi_{lat}(\bold{q}) = \frac{\chi_{lat}^{(0)}(\bold{q})}{1+2\tilde{\lambda}_{\bold{q}}\frac{\chi(\bold{q})}{e^2\nu(\varepsilon_F)}}

会随着其分母中负的磁化率 \chi(\bold{q}) 的增加而增加，即晶格的敏感性会提高甚至是发散，一个等价的观点是声子的频率会降低趋近于 0 ，即所谓的声子冷冻(frozen phonon)，声子的运动速度会降下来，产生一个静态的扭曲，对应于一个波矢，这一相变也被叫做 Perierls transition 。

\chi(2k_F) 的温度依变性

我们首先从一个一维金属的玩具模型开始，该效应在 q = 2k_F 最强，此刻我们有一个完美的nesting。我们需要计算在该波矢下的介质磁化率的易变形

\chi(2k_F) = \frac{2e^2}{2b^2}\frac{1}{2\pi}\int_{-\infty}^{\infty} \frac{f(\varepsilon_k)-f(\varepsilon_{k+2k_F})}{\varepsilon_k - \varepsilon_{k+2k_F}}

\varepsilon_k = \frac{\hbar^2k^2}{2m}

r然后我们有

\varepsilon_k - \varepsilon_{k+2k_F} = -\frac{2\hbar^2k_F}{m}(k+k_F)

积分的部分没办法给出解析解，不过我们可以在 \varepsilon_F>>T 的时候给出一个近似解，在该情况下，我们在下图中绘制出 A(k) = -\frac{1}{\varepsilon_k - \varepsilon_{k+2k_F}} 以及 B(k) = f(\varepsilon_k) - f(\varepsilon_{k+2k_F})

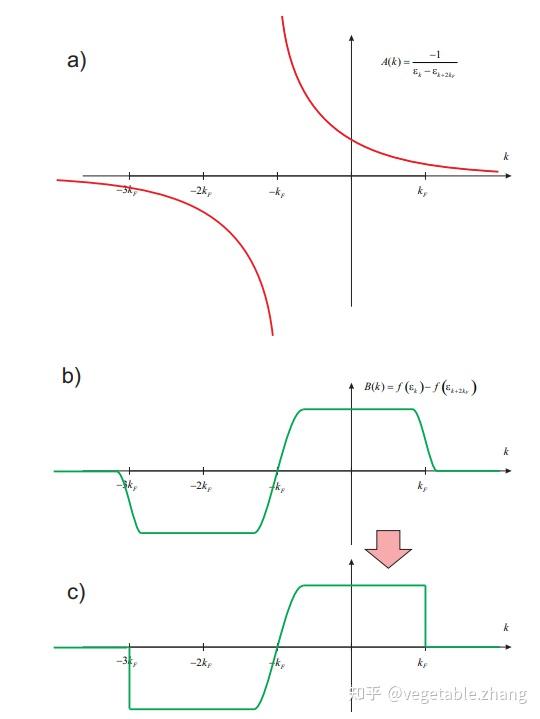
由于 A(k) 和 B(k) 一个发散一个趋近于 0 ，我们进一步处理

\varepsilon_k - \varepsilon_{k_F} = -\frac{\hbar^2k_F}{m}(k+k_F)

\varepsilon_{k+2k_F} - \varepsilon_F \approx \frac{\hbar^2 k_F}{m}(k+k_F)

f(\varepsilon_k)-f(\varepsilon_{k+2k_F})\approx \tanh{\bigg[\frac{\hbar^2 k_F}{2mk_BT}(k+k_F)\bigg]}

对于 B(k) ，因为其与 A(k) 的乘积在 k>k_F 以及 k<-3k_F 时几乎趋近于 0 ，我们做一个近似，令其乘上一个在 (-3k_F, k_F) 为 1 的方波（其余地方为0），如上图（c）所示，这样我们有

\begin{align*} \chi(2k_F) &\approx -\frac{e^2}{\pi b^2} \int_{-3k_F}^{k_F}dk \frac{\tanh{[\frac{\hbar^2k_F}{2mk_BT}(k+k_F)]}}{\frac{\hbar^2k_F}{m}(k+k_F)} \\ &= -\frac{e^2m}{\pi \hbar^2k_F b^2}\int_0^{\frac{\hbar^2k_F^2}{mk_BT}}dx \frac{\tanh{x}}{x} \\&\approx -\frac{e^2 m}{\pi \hbar^2 k_F b^2} \ln{\bigg(\frac{1.14\hbar^2 k_F^2}{mk_BT}\bigg)} \end{align*}

在一维的情况下， \nu(\varepsilon_F) =\frac{2m}{\pi\hbar^2k_Fb^2} ，于是我们有

\chi(2k_F) = -\frac{e^2 \nu(\varepsilon_F)}{2}\ln{\bigg(\frac{2.28 \varepsilon_F}{k_BT}\bigg)}

软声子

\chi(q = 2k_F) 的温度依变性可以等同于一个Kohn异常的温度依变形，根据声子的等效频率

\Omega_{\bold{q}}^2 = \omega_{\bold{q}}^2 \bigg[1+2\tilde{\lambda}_{\bold{q}}\frac{\chi(\bold{q})}{e^2\nu(\varepsilon_F)}\bigg]

我们有

\Omega_{2k_F}^2 = \omega_{2k_F}^2\bigg[1-\tilde{\lambda}_{2k_F}\ln{\bigg(\frac{2.28\varepsilon_F}{k_B T}\bigg)}\bigg]

这一现象在实验中也被观察到过。定量分析，一维金属在不同温度下的Kohn anomaly由下图绘出。

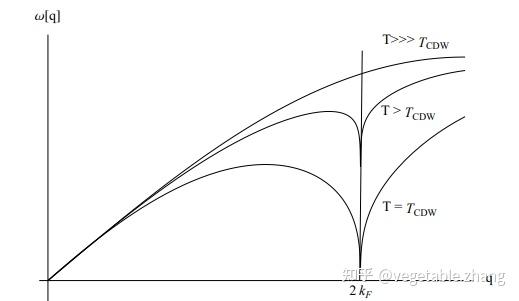
相变温度

CDW的相变发生在晶格的敏感性 q = 2k_F 发散的时候，或者等价来说，当绳子的频率在 T = T_c 以及该波矢趋近于零时，也就是当

\chi_{lat}(\bold{q}) = \frac{\chi_{lat}^{(0)}(\bold{q})}{1+2\tilde{\lambda}_{\bold{q}}\frac{\chi(\bold{q})}{e^2\nu(\varepsilon_F)}}

的分母等于 0 时，我们有

k_B T_{CDW} = 2.28 \cdot \varepsilon_F \exp(-\frac{1}{\tilde{\lambda}_{2k_F}})

屏蔽的

上述计算实际上是基于周期性的晶格势场，随着 \chi_{2k_F} 变大，离子势场的 2k_F 的傅里叶分量会被严重的屏蔽掉，这一现象可以使用我们在 上一章 关于电子屏蔽时的讨论来处理，即使用如下势场公式

\Phi = \phi \bigg(1 - \frac{\chi(\bold{q})}{\varepsilon_0 q}\bigg)^{-1}

因在对于任意波矢 \bold{q}

|\tilde{U}_{\bold{q}}|^2 = |U_\bold{q}|^2\bigg(1 - \frac{\chi(\bold{q})}{\varepsilon_0 q^2}\bigg)^{-2}

其中 U 是未屏蔽的电子势场。这仅仅是离子核的库伦势场，与温度无关，我们因此可以定义未屏蔽的电子声子耦合常数为

\lambda_{\bold{q}} = \frac{e^2}{2M\omega_q^2}(\bold{q}\cdot \hat{\bold{u}})^2 |U_\bold{q}|^2 V_0 \nu(\varepsilon_F)

我们可以放心该常数为温度依变的，形成想变得条件是

\frac{2\lambda_\bold{q}}{e^2 \nu(\varepsilon_F)} \frac{\chi_{\bold{q}}}{\bigg(1-\frac{\chi(\bold{q})}{\varepsilon_0 q^2}\bigg)^2} = -1

上式左边的第二部分，当 |\chi(\bold{q})| 很小时几乎等于 \chi(\bold{q}) ，当 |\chi(\bold{q})| 很大时就趋近于 1/\chi(\bold{q}) ，在 \chi(\bold{q}) = -\varepsilon_0 q^2 时达到最小值。因此，上式只有当

\lambda_\bold{q}\geq \frac{2e^2\nu(\varepsilon_F)}{\varepsilon_0 q^2} = \frac{2K^2}{q^2}

其中 \frac{1}{K} 是Thomas-Fermi屏蔽长度。将该式用到nesting vector q = 2k_F 是，我们有

2\lambda_{\bold{q}} \geq (K/k_F)^2

通过以上讨论我们有两个结果：

1. 如果耦合项过弱，相变不会发生，绳子的频率在 2k_F 会随着温度的降低而减小，达到一个正的最小值然后继续增加。另一方面，如果 2\lambda_{\bold{q}}>>(K/k_F)^2 该值会在某些温度达到 0 ，形成CDW相变。
2. 对于很强的耦合，屏蔽作用可以忽略掉，通过 k_B T_{CDW} = 2.28 \cdot \varepsilon_F \exp(-\frac{1}{\tilde{\lambda}_{2k_F}}) 我们可以得到一个很好的相变温度的估计

CDW态

前面的所有讨论都是为了说明费米面附近的电子可以驱动某种特定横波频率的声子趋近于 0 ，这表面了一个发散的弹性敏感性，以及一个二阶的相变点。我们目前没有完成的是定量地描述该相变的有序度，或者描述费米液体在相变点上下的行为。我们并没有证明CDW相变在能量上是被倾向于形成的。

有序参数

我们首要做的是确定CDW的有序参数。我们可以很自然的想到用离子晶格格点的位移幅度来表示，这样的一个位移，以及一个相应的周期调节的电子密度如下图所示

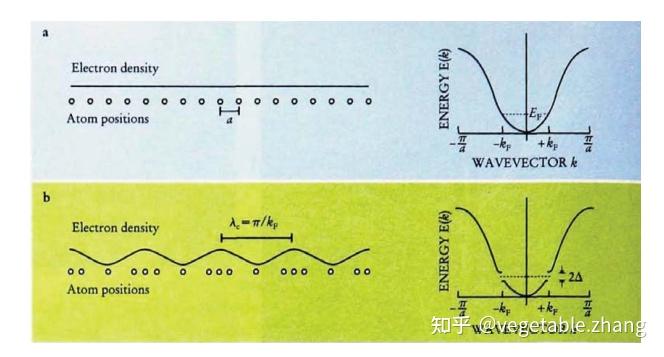
离子的位移通常很小，大概是晶格常数的一百分之一或者一千分之一。注意，尽管如此，位移波依然可以通过其相位被表征。我们可以考虑一个复振幅

u = |u|\exp{(i\phi)}

实际上，晶格的位移矢量

\bold{u}_j = \bold{u} \exp{(i\bold{q}\bold{R}_j)}+c.c.

可以写作

\bold{u}(\bold{r}) = 2|u|\bold{\hat{u}}\cos{(i\bold{q}\bold{r}+\phi)}

接下来我们关注晶格扭曲对费米面的影响，这个时候，我们选择电子势场的复振幅作为有序参数，该复振幅由晶格扭曲造成，和离子位移作为有序参数完全等价，而且更方便

\Delta = -ie(\bold{\bold{q}\hat{u}})U_{\bold{q}}u

再次强调， \Delta = |\Delta|\exp{(i \mathrm{Arg}(\Delta))} 是一个复数的有序参数，包含了由与晶格扭曲造成的静电势能的幅度和相位。

CDW

我们现在考虑晶格扭曲造成的静电周期势场，由第一节关于 “晶格畸变对电子影响” 那一节的公式

\int \mathrm{d} \bold{r}' \bold{u}(\bold{r}')\nabla\tilde{U}(\bold{r}'-\bold{r}) = \oint \tilde{U}(\bold{r}'-\bold{r})\bold{u}(\bold{r}') \mathrm{d}\bold{s} - \int\mathrm{d}\bold{r'} \tilde{U}(\bold{r}'-\bold{r})\nabla \bold{u}(\bold{r}') = -i(\bold{q}\bold{u})\tilde{U}_{\bold{q}} \exp{(i\bold{q}\bold{r})}+c.c.

可知

\Delta(r) = \Delta \exp{(2irk_F)}+\Delta^* \exp{(-2irk_F)}

我们很知道一个周期性势场对一个自由粒子耗散关系的影响，这个问题在最初级的固体物理课里已经得到解决。为了完整性，我们重新讨论一下下，我们将周期性势场的每一个分量都看作一个微扰，对于一个单电子状态 |k\rangle ，矩阵项有

\langle k + 2k_F |\hat{\Delta}|k\rangle = \Delta

我们很容易想到去写出 \varepsilon_k 的二阶修正，在处理 k = \pm k_F 处的能带，我们必须考虑微扰项导致的简并，我们需要处理下面的矩阵

\begin{vmatrix} \varepsilon_k - E & \Delta \\ \Delta^* & \varepsilon_{k\pm2k_F}-E \end{vmatrix}

上式中 \varepsilon_{k} = \frac{\hbar^2 k^2}{2m} 是自由电子的耗散关系，通过求解上式我们有

\begin{align*} \tilde{\varepsilon}_k = \varepsilon_k &- \frac{1}{2}\bigg[\varepsilon_k - \varepsilon_{k+2k_F}\pm\sqrt{(\varepsilon_k - \varepsilon_{k+2k_F})^2+4|\Delta|^2} \bigg] \\ &-\frac{1}{2}\bigg[\varepsilon_k - \varepsilon_{k-2k_F}\pm\sqrt{(\varepsilon_k - \varepsilon_{k-2k_F})^2+4|\Delta|^2} \bigg] \end{align*}

由上式导致的结果如下所示，原本自由电子的耗散曲线在 \pm k_F 附近产生了一个 2\Delta 的带宽。注意到费米能级在能带中央，CDW态实际上是一个绝缘体态。

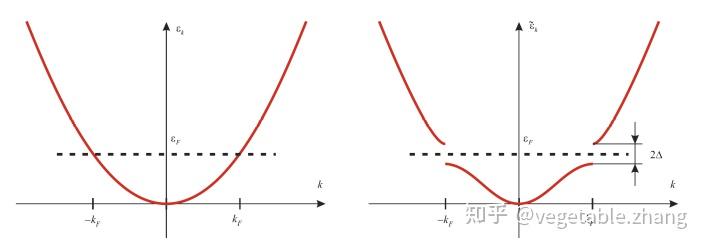
为了更好的描述费米面附近的耗散关系，我们引入

\epsilon_k = \varepsilon_k - \varepsilon_F

在费米面 \pm k_F 附近

\epsilon_{k\sim \pm k_F}\approx -\epsilon_{k\mp2k_F}

然后我们有

\tilde{\epsilon}_{k}\approx \pm \sqrt{\epsilon_k^2+|\Delta|^2}

费米面附近的DOS如下图所示

\tilde{\nu}(\tilde{\epsilon}) = \nu(\epsilon)\bigg(\frac{\mathrm{d\tilde{\epsilon}}}{\mathrm{d}\epsilon}\bigg)^{-1}

代入 \tilde{\epsilon}_{k}\approx \pm \sqrt{\epsilon_k^2+|\Delta|^2} 后，在 \pm k_F 附近我们有

\tilde{\nu} (\epsilon)\approx \nu(\varepsilon) \left \{ \begin{array}{**lr**} 0, &|\epsilon|<|\Delta| \\ \frac{|\epsilon|}{\sqrt{\epsilon^2 - |\Delta|^2}}, &|\epsilon|>|\Delta| \end{array} \right.

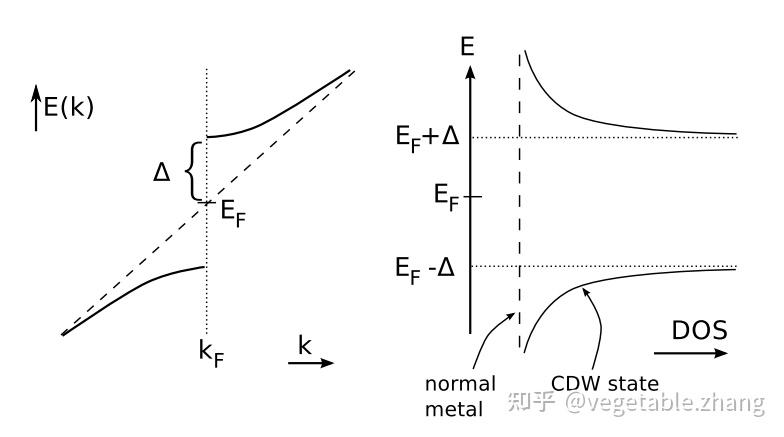
\Delta 大小的估计

当 T\to 0 时我们可以估计CDW带隙的大小。我们首先注意到新打开的能带降低了费米面的能量，这对静电势能的改变可以由下式给出

E_{el} = \frac{Vk_F}{\pi b^2}\bigg[2\bigg(\sqrt{|\Delta|^2 + 16\varepsilon_F^2}-4\varepsilon_F\bigg)+\frac{|\Delta|^2}{4\varepsilon_F} \ln{\frac{\sqrt{|\Delta|^2+16\varepsilon_F^2}+4\varepsilon_F}{\sqrt{|\Delta|^2+16\varepsilon_F^2}-4\varepsilon_F}}\bigg]

如果打开的能带够小， \Delta << \varepsilon_F 我们有

E_{el} = -\frac{1}{2}\nu(\varepsilon_F)V\Delta^2\bigg[\frac{1}{2}-\ln{\frac{\Delta}{8\varepsilon_F}}\bigg]

这个能量必须通过晶格的弹性势能被平衡掉，根据 \Delta = ie(2k_Fu)U_{2k_F} ，每个晶胞内我们有

\delta E_{lat} = NM\omega_{\bold{q}}^2 |u|^2 = \frac{NM \omega_{\bold{q}}^2}{e^2(\bold{q}\bold{\hat{u}})^2U_{\bold{q}}^2}|\Delta|^2 = V\frac{\nu(\varepsilon_F)}{2\lambda_{2k_F}}|\Delta|^2

这就给出了我们CDW状态可以稳定的条件

E_{total} = \frac{1}{2}V\nu(\varepsilon_F)|\Delta|^2\bigg[\frac{1}{\lambda_{2k_F}}-\frac{1}{2}+\ln{\bigg(\frac{8\varepsilon_F}{|\Delta|}\bigg)}\bigg]<0

当 \Delta 很小的时候上述条件基本上都是成立的，因此一维的金属态的CDW本质上都是不稳定的。这一结论首先由 Pierels给出， T\to 0 时的 \Delta 的平衡之通过求解 \frac{\mathrm{d}E_{tot}}{\mathrm{d}\Delta } = 0 得到：

|\Delta| = 8\varepsilon_F \exp{\bigg(-\frac{1}{\lambda_{2k_F}}\bigg)}

和实验数据对比

通过上述理论，我们可以估算以下两个物理量 T_{CDW} 和 \Delta

k_B T_{CDW} = 2.28 \cdot \varepsilon_F \exp\bigg(-\frac{1}{\tilde{\lambda}_{2k_F}}\bigg)

|\Delta| = 8\varepsilon_F \exp{\bigg(-\frac{1}{\lambda_{2k_F}}\bigg)}

通过上述两式可以得到 \frac{2\Delta}{k_B T_{CDW}} \approx 7.0 ，在实验中 \Delta 可以通过光谱测出，或者通过直流导电率和温度的关系推出（一会儿解释），我们给出一些材料的 T_{CDW} 以及 2\Delta (所有能量单位都为K)

材料	CDW相变温度	能带宽度（2倍）	\Delta_{optical}	\lambda_{el-phonon}
KCP	189	1400	1700	0.3
K0.3MoO3	183	920	1400	0.34
TaS3	215	1600	1800	0.65
NbS3	145以及59	700	\	0.53

大部分实验中 2\Delta 和 T_{CDW} 的关系都是符合我们前面推论的。

金属态和CDW态的电流

我们在下图中讨论金属和CDW态下的电子状态以及加了电场后的状态。下图a表示一个没有外场的金属中电子的状态，对应图中红色加粗部分；在加了电场后，电子沿着电场方向的动量增加，表现在图b的红色带向右漂移；电子运动中需要和金属中的晶格、杂质散射（否则电流将会无穷大），散射需要电子在动量的另一侧有可供散射到的状态，比如图c中右边漂上去的电子可以散射到左边的态，这样最后散射和电场平衡就形成了稳定的电流。由于散射造成的能量释放就对应焦耳热。电场越大，电子状态漂移的越多，左右两侧的状态数量差别就越大，最后形成的电流也越大。如果散射率是一个常数的话，只需要终态的数量就能确定弛豫率，最后形成的稳定电流正比于电场强度，这就是欧姆定律。

上述讨论针对CDW就会出现问题。由于周期性的晶格畸变导致电子的状态存在一个能带，在无外场下电子的能带结构所示以及分布如上图d所示，加完电场后能带向右漂移。与一般半导体或绝缘体（对应图e，即电子的动量增加，但只会到下一个布里渊区，而不是跃迁到更高能级，然后散射形成电流）不一样的是，CDW中晶格格点上的离子运动也要考虑进来，在考虑了格点运动后，系统提供的电子状态也会发生飘移，如图f所示，最后电子还是能获得新的可供散射到的状态，然后形成电流。

但由于晶格格点上离子的运动还会与杂质作用，虽然形成畸变但最后还是会定在某个状态，也会产生能量消耗，即焦耳热。因此CDW态和超导状态还是不一样的。CDW态会被钉扎在杂志上并且不再变化，最后材料还是绝缘体。然而通过施加足够强的电场，我们可以让离子局部运动一下，从而不被钉扎，然后形成电流，这一现象也在试验中被观测到。