因果推断笔记——因果图建模之微软开源的EconML(五)


1 EconML介绍
GITHUB :
econml DOC:
1.1 EconML介绍
机器学习最大的promise之一是在许多领域实现决策的自动化。 许多数据驱动的决策场景的核心问题是对heterogeneous treatment effects的估计,也即: 对于具有特定特征集的样本,干预对输出结果的causal effect是什么? 简言之,这个Python工具包旨在: - 测量某些干预变量T对结果变量Y的causal effect - 控制一组特征X和W,来衡量causal effect如何随X的变化而变化
这个Python工具包旨在测量某些干预变量T对结果变量Y的causal effect,控制一组特征X和W,来衡量causal effect如何随X的变化而变化。
这个包里实现的方法适用于观察的数据集(非实验或历史)。为了使估计结果具有因果解释,一些算法假设数据中没有未观察到的混杂因子(即同时对T和Y产生影响的因子均被包含在X,W中),而其他一些算法则假设可以使用工具变量Z(即观测变量Z对干预T有影响,但对结果变量Y没有直接影响)。 并且包中的大多数算法都可以提供置信区间和推断结果。
我们将概述最近将机器学习与因果推理结合起来的方法,以及机器学习给因果推理估计方法带来的重要统计性能。 相比DoWhy,EconML借助一些更复杂的机器学习算法来进行因果推断。在EconML中可以使用的因果推断方法有:
- 双机器学习(Double Machine Learning)。
- 双重鲁棒学习(Doubly Robust Learner)。
- 树型学习器(Forest Learners)。
- 元学习器(Meta Learners)。
- 深度工具变量法(Deep IV).
- 正交随机树(Orthogonal Random Forest)
- 加权双机器学习(Weighted Double Machine Learning)
我们还将概述置信区间构建(例如自举、小袋自举、去偏lasso)、可解释性(形状值、树解释器)和策略学习(双鲁棒策略学习)的方法。 EconML希望做到以下几点:
- 实现同时涉及计量经济学和机器学习的最新方法
- 保持对effect heterogeneity建模的灵活性(通过随机森林、boosting、lasso和神经网络等技术),同时- 保留所学模型的因果解释,并同时提供有效的置信区间
- 使用统一的API - 构建标准的Python包以用于机器学习和数据分析
1.2 一些理论解答
参考:
的【3.0.2 章节】
异质处理效应 (Heterogenous treatment effects,HTE) 简单理解就是按某些规律进行分组之后的ATE,也就是“条件平均处理效应”(Conditional Average Treatment Effect,CATE) 每个子组的平均处理效应被称为“条件平均处理效应”(Conditional Average Treatment Effect,CATE) ,也就是说,每个子组的平均处理效应被称为条件平均处理效应,以子组内的分类方式为条件。
1.3 常规CATE的估计器
在econML中,“条件平均处理效应”(Conditional Average Treatment Effect,CATE) 的四种估计方式:
- 双机器学习(Double Machine Learning)。
- 双重鲁棒学习(Doubly Robust Learner)。
- 元学习器(Meta Learners)。
- 正交随机树(Orthogonal Random Forest)
DML的几种方法包括:
- econml.dml.DML( , model_y, model_t, model_final) # 基础双重ML的模型
- econml.dml.LinearDML( [, model_y, model_t, …]) # 线性估计器
- econml.dml.SparseLinearDML( [, model_y, …]) # 稀疏线性估计器
- econml.dml.CausalForestDML( [, model_y, …]) # 因果树
- econml.dml.NonParamDML(*, model_y, model_t, …) # 非参数ML估计器, that can have arbitrary final ML models of the CATE.
双重鲁棒学习(Doubly Robust Learner)几种方法:
- econml.dr.DRLearner( [, model_propensity, …])
- econml.dr.LinearDRLearner( [, …])
- econml.dr.SparseLinearDRLearner( [, …])
- econml.dr.ForestDRLearner( [, …])
CATE estimator that uses doubly-robust correction techniques to account for covariate shift (selection bias) between the treatment arms.
元学习器(Meta Learners)四种方法:
- econml.metalearners.XLearner( , models[, …])
- econml.metalearners.TLearner( , models[, …])
- econml.metalearners.SLearner( , overall_model)
- econml.metalearners.DomainAdaptationLearner( , …) 元算法,使用领域适应技术来解释
正交随机树(Orthogonal Random Forest) 的两种方法:
- econml.orf.DMLOrthoForest( [, n_trees, …])
- econml.orf.DROrthoForest( [, n_trees, …])
1.4 IV工具变量 + CATE的估计器
Double Machine Learning (DML) IV的几种方法:
- econml.iv.dml.OrthoIV( [, model_y_xw, …]) 用IV实现正交/双ml方法进行CATE估计
- - econml.iv.dml.NonParamDMLIV(*[, model_y_xw, …]) 非参数DMLIV的基类,允许在DMLIV算法的最后阶段采用任意平方损耗的ML方法。
Doubly Robust (DR) IV 稳健+IV几种方法:
- econml.iv.dr.DRIV(*[, model_y_xw, …])
- econml.iv.dr.LinearDRIV(*[, model_y_xw, …])
- econml.iv.dr.SparseLinearDRIV(*[, …]) # 稀疏
- econml.iv.dr.ForestDRIV(*[, model_y_xw, …]) # 因果树
- econml.iv.dr.IntentToTreatDRIV(*[, …])
- econml.iv.dr.LinearIntentToTreatDRIV(*[, …]) # 为线性意图处理A/B测试设置实现DRIV算法
DeepIV方法: - econml.iv.nnet.DeepIV(*, n_components, m, h, …)
Sieve Methods 的几种方法:
- econml.iv.sieve.SieveTSLS(*, t_featurizer, …)
- econml.iv.sieve.HermiteFeatures(degree[, …])
- econml.iv.sieve.DPolynomialFeatures([…])
1.5 动态处理效应的估计器
- econml.dynamic.dml.DynamicDML(*[, model_y, …]) 用于动态处理效果估计的CATE估计器。
2 智能营销案例一:(econml)不同优惠折扣下的用户反应
参考:
2.1 背景

如今,商业决策者依靠评估干预的因果效应来回答有关策略转变的假设问题,比如打折促销特定产品、向网站添加新功能或增加销售团队的投资。 然而,人们越来越感兴趣的是了解不同用户对这两种选择的不同反应,而不是学习是否要针对所有用户的特定干预采取行动。 识别对干预反应最强烈的用户特征,有助于制定规则,将未来用户划分为不同的群体。 这可以帮助优化政策,使用最少的资源,获得最大的利润。
在本案例研究中,我们将使用一个个性化定价示例来解释EconML库如何适应这个问题,并提供健壮可靠的因果解决方案。
目的是了解不同收入水平人群的需求的异质性价格弹性,了解哪个用户对小折扣的反应最强烈。 此外,他们的最终目标是确保,尽管对一些消费者降低了价格,但需求有足够的提高,以提高整体收入。
EconML的基于“DML”的估计器可用于获取现有数据中的折扣变化,以及一组丰富的用户特性,以估计随多个客户特性而变化的异构价格敏感性。
然后,EconML的可解释性的两个函数:
- SingleTreeCateInterpreter 提供了一个presentation-ready总结的关键特性,解释折扣最大的响应能力的差异,
- SingleTreePolicyInterpreter - 建议谁应该获得折扣政策为了增加收入(不仅需求),这可能有助于该公司在未来为这些用户设定一个最优价格。
2.2 数据准备与理解
# Some imports to get us started
# Utilities
import os
import urllib.request
import numpy as np
import pandas as pd
# Generic ML imports
from sklearn.preprocessing import PolynomialFeatures
from sklearn.ensemble import GradientBoostingRegressor
# EconML imports
from econml.dml import LinearDML, CausalForestDML
from econml.cate_interpreter import SingleTreeCateInterpreter, SingleTreePolicyInterpreter
import matplotlib.pyplot as plt
%matplotlib inline
# Import the sample pricing data
file_url = "https://msalicedatapublic.blob.core.windows.net/datasets/Pricing/pricing_sample.csv"
train_data = pd.read_csv(file_url)
# Define estimator inputs
Y = train_data["demand"] # outcome of interest
T = train_data["price"] # intervention, or treatment
X = train_data[["income"]] # features
W = train_data.drop(columns=["demand", "price", "income"]) # confounders
# Get test data
X_test = np.linspace(0, 5, 100).reshape(-1, 1)
X_test_data = pd.DataFrame(X_test, columns=["income"])
其中
train_data
是
10000*11
完整的数据集,而
X_test_data
是新生成的一列自变量
X
, 这里可以看到,test数据集 其实不用捎上混杂因子的
W
变量们,也不用额外生成干预变量
T
数据格式为:
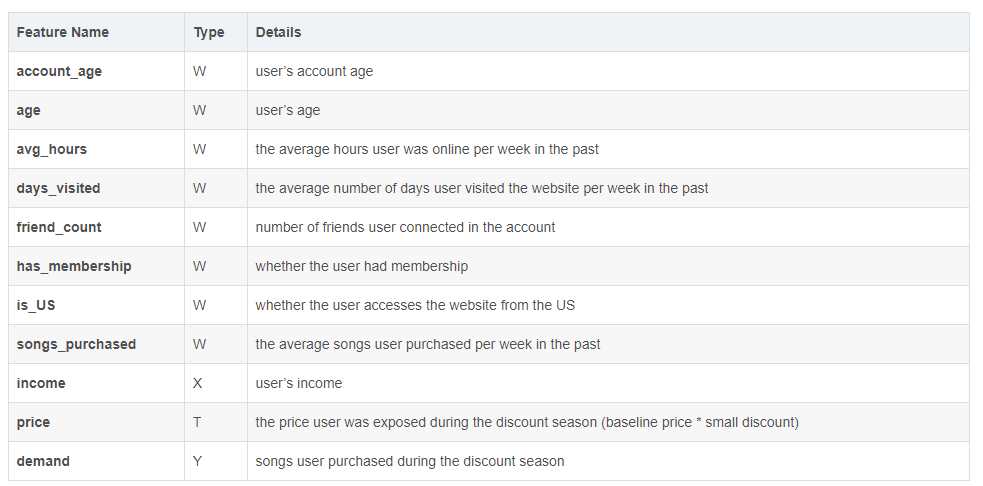
数据集*有~ 10000个观察,包括9个连续和分类变量,代表用户的特征和在线行为历史,如年龄,日志收入,以前的购买,每周以前的在线时间等。 为了保护公司的隐私,我们这里以模拟数据为例。数据是综合生成的,特征分布与真实分布不一致。 然而,特征名称保留了它们的名称和含义.
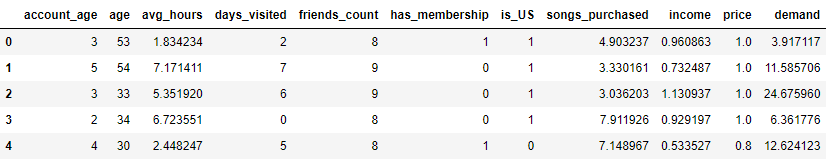
这里来盘一下具体的因果逻辑:
- 其他变量:account_age ~ songs_purchased - W - 混杂因子
- income - X - 考察变量 - 用户收入
- demand - Y - outcome - 销量
-
Price - T - 干预,折扣,取值为
[1,0.9,0.8],根据下面的公式的来

2.3 生成假的Groud Truth的估计效应
估计效应的对比,此时没有一个标准答案,所以这里就搞了一个手算版本,当作真实的估计量,来进行对比。
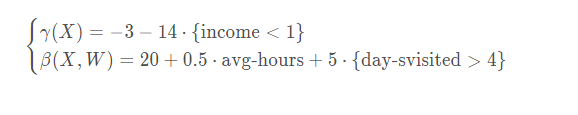
最终要算的是价格弹性elasticity
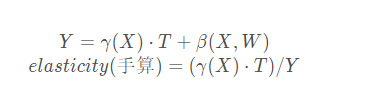
当然,在实际计算中有取对数的操作,公式会变成:
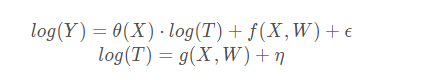
整体生成手算的估计效应:
# Define underlying treatment effect function given DGP
def gamma_fn(X):
return -3 - 14 * (X["income"] < 1)
def beta_fn(X):
return 20 + 0.5 * (X["avg_hours"]) + 5 * (X["days_visited"] > 4)
def demand_fn(data, T):
Y = gamma_fn(data) * T + beta_fn(data)
return Y
def true_te(x, n, stats):
if x < 1:
subdata = train_data[train_data["income"] < 1].sample(n=n, replace=True)
else:
subdata = train_data[train_data["income"] >= 1].sample(n=n, replace=True)
te_array = subdata["price"] * gamma_fn(subdata) / (subdata["demand"])
if stats == "mean":
return np.mean(te_array)
elif stats == "median":
return np.median(te_array)
elif isinstance(stats, int):
return np.percentile(te_array, stats)
# Get the estimate and range of true treatment effect
truth_te_estimate = np.apply_along_axis(true_te, 1, X_test, 1000, "mean") # estimate
truth_te_upper = np.apply_along_axis(true_te, 1, X_test, 1000, 95) # upper level
truth_te_lower = np.apply_along_axis(true_te, 1, X_test, 1000, 5) # lower level
这里的
truth_te_estimate
就是最终估计数字了,公式即为:
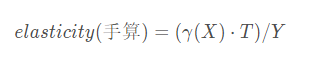
te_array = subdata["price"] * gamma_fn(subdata) / (subdata["demand"])2.4 X~Y 分析:线性估计器LinearDML
# Get log_T and log_Y
log_T = np.log(T)
log_Y = np.log(Y)
# Train EconML model
est = LinearDML(
model_y=GradientBoostingRegressor(),
model_t=GradientBoostingRegressor(),
featurizer=PolynomialFeatures(degree=2, include_bias=False),
est.fit(log_Y, log_T, X=X, W=W, inference="statsmodels")
# Get treatment effect and its confidence interval 得到治疗效果及其置信区间
te_pred = est.effect(X_test)
# 因为是配对实验,PSM,那就是 ps(y=1) - ps(y=0),每个人都有,
# 后面求ATE的时候,会进行平均
te_pred_interval = est.effect_interval(X_test) # 置信区间 上限与下限
# Compare the estimate and the truth
plt.figure(figsize=(10, 6))
plt.plot(X_test.flatten(), te_pred, label="Sales Elasticity Prediction")
plt.plot(X_test.flatten(), truth_te_estimate, "--", label="True Elasticity")
plt.fill_between(
X_test.flatten(),
te_pred_interval[0],
te_pred_interval[1],
alpha=0.2,
label="95% Confidence Interval",
plt.fill_between(
X_test.flatten(),
truth_te_lower,
truth_te_upper,
alpha=0.2,
label="True Elasticity Range",
plt.xlabel("Income")
plt.ylabel("Songs Sales Elasticity")
plt.title("Songs Sales Elasticity vs Income")
plt.legend(loc="lower right")
先来解读一下步骤,
LinearDML
初始化之后,就直接
fit
建模, 这里初始化了
model_y + model_t
两个模型,也就是在估计器里,当出现了X/T/W/Y拟合了两个模型:
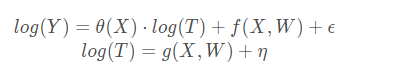
此时可以说,
X|T~Y
的异质性处理效应就是弹性 (~~笔者喜欢在这里把X叫做异质变量,异质处理效应在这里就是需求弹性~~ ), 直接计算处理效应:
est.effect(X_test)
,这里可以看到估计效应只需要
X(income)
一列就可以了, 同时给到处理效应的区间估计
effect_interval
, 之后就是把,手算的真效应估计量,pred预测估计量进行对比:
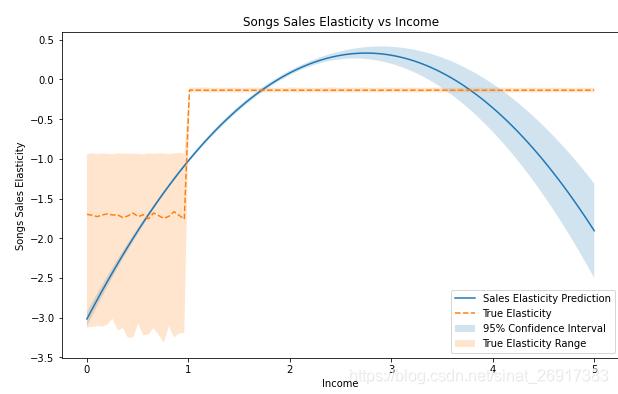
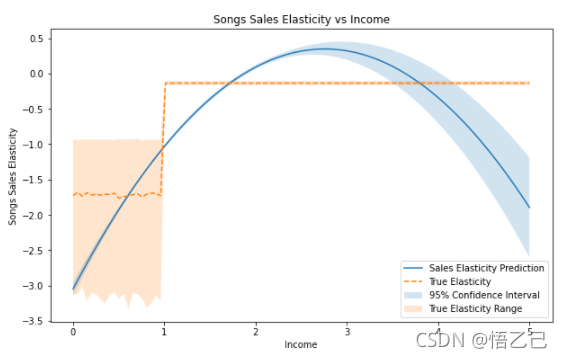
从手算的
弹性~income
的关系来看,是一条非线性曲线,当收入小于1时,弹性在-1.75左右,当收入大于1时,有一个较小的负值。 模型拟合的是二次项的函数,拟合不是很好。 但它仍然抓住了总体趋势:弹性是负的,如果人们有更高的收入,他们对价格变化的敏感度就会降低。
# Get the final coefficient and intercept summary
est.summary()输出结果:
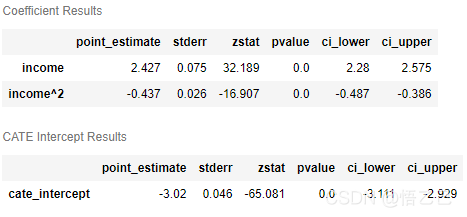
“线性dml”估计器也可以返回最终模型的系数和截距的总结,包括点估计、p值和置信区间。 由上表可知, $income$ 具有正效应, ${income}^2$ 具有负效应,两者在统计学上都是显著的。
2.5 X~Y 分析:非线性估计器:因果树CausalForestDML
# Train EconML model
est = CausalForestDML(
model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor()
est.fit(log_Y, log_T, X=X, W=W, inference="blb")
# Get treatment effect and its confidence interval
te_pred = est.effect(X_test)
te_pred_interval = est.effect_interval(X_test)
# Compare the estimate and the truth
plt.figure(figsize=(10, 6))
plt.plot(X_test.flatten(), te_pred, label="Sales Elasticity Prediction")
plt.plot(X_test.flatten(), truth_te_estimate, "--", label="True Elasticity")
plt.fill_between(
X_test.flatten(),
te_pred_interval[0],
te_pred_interval[1],
alpha=0.2,
label="95% Confidence Interval",
plt.fill_between(
X_test.flatten(),
truth_te_lower,
truth_te_upper,
alpha=0.2,
label="True Elasticity Range",
plt.xlabel("Income")
plt.ylabel("Songs Sales Elasticity")
plt.title("Songs Sales Elasticity vs Income")
plt.legend(loc="lower right")
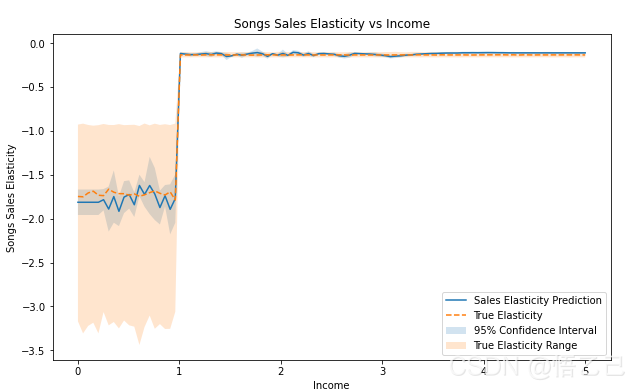
我们注意到,这个模型比“线性dml”更适合,95%置信区间正确地覆盖了真实的处理效果估计,并捕捉了收入约为1时的变化。 总体而言,该模型表明,低收入人群比高收入人群对价格变化更加敏感。
2.6 X|T~Y分析:SingleTreeCateInterpreter哪些用户比较积极/消极
EconML包括可解释性工具,以更好地理解治疗效果。
治疗效果可能很复杂,但我们通常感兴趣的是一些简单的规则,这些规则可以区分哪些用户对提议的变化做出积极回应,哪些用户保持中立,哪些用户做出消极回应。
EconML SingleTreeCateInterpreter通过训练由任何EconML估计器输出的处理效果的单一决策树来提供可解释性。
intrp = SingleTreeCateInterpreter(include_model_uncertainty=True, max_depth=2, min_samples_leaf=10)
intrp.interpret(est, X_test)
plt.figure(figsize=(25, 5))
intrp.plot(feature_names=X.columns, fontsize=12)在下图中,我们可以看到暗红色的用户(income < 0.48)对折扣反应强烈,白色的用户对折扣反应轻微。
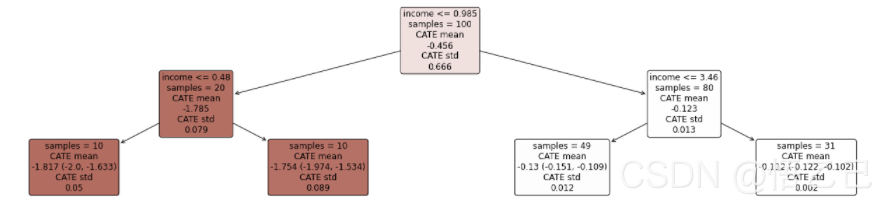
2.7 T~X分析:SingleTreePolicyInterpreter 什么收入的人该打折
intrp = SingleTreePolicyInterpreter(risk_level=0.05, max_depth=2, min_samples_leaf=1, min_impurity_decrease=0.001)
intrp.interpret(est, X_test, sample_treatment_costs=-1)
plt.figure(figsize=(25, 5))
intrp.plot(feature_names=X.columns, treatment_names=["Discount", "No-Discount"], fontsize=12)随着价格的降低,只有当 $\theta(X)+1<0$ 时,收入才会增加。 因此,我们在这里设置' sample_treatment_cast=-1 ',以了解 我们应该给哪种类型的客户一个小的折扣,以使收入 最大。
EconML库包括“SingleTreePolicyInterpreter”等策略可解释性工具,该工具可以计算治疗成本和治疗效果,以了解关于哪些客户可以获利的简单规则。 从下图中我们可以看到,模型建议对收入低于$0.985$的人给予折扣,对其他人给予原价。
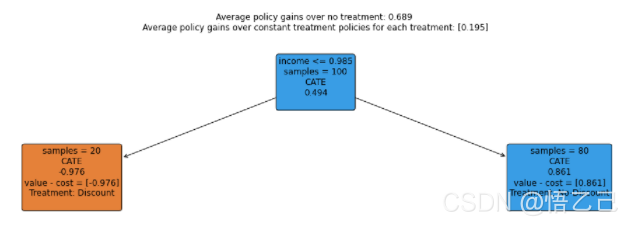
2.8 干预后的结果对比(该打折的人打折后)
现在,让我们将我们的政策与其他基准政策进行比较, 我们的模型告诉我们哪些用户可以给予小的折扣,在这个实验中,我们会为这些用户设定10%的折扣级别。 由于模型被错误地指定,我们不会期望有大折扣的好结果。 在这里,因为我们知道基本的真相,所以我们可以评估这个政策的价值。
# define function to compute revenue
def revenue_fn(data, discount_level1, discount_level2, baseline_T, policy):
policy_price = baseline_T * (1 - discount_level1) * policy + baseline_T * (1 - discount_level2) * (1 - policy)
demand = demand_fn(data, policy_price)
rev = demand * policy_price
return rev
policy_dic = {}
# our policy above
policy = intrp.treat(X)
policy_dic["Our Policy"] = np.mean(revenue_fn(train_data, 0, 0.1, 1, policy))
## previous strategy
policy_dic["Previous Strategy"] = np.mean(train_data["price"] * train_data["demand"])
## give everyone discount
policy_dic["Give Everyone Discount"] = np.mean(revenue_fn(train_data, 0.1, 0, 1, np.ones(len(X))))
## don't give discount
policy_dic["Give No One Discount"] = np.mean(revenue_fn(train_data, 0, 0.1, 1, np.ones(len(X))))
## follow our policy, but give -10% discount for the group doesn't recommend to give discount
policy_dic["Our Policy + Give Negative Discount for No-Discount Group"] = np.mean(revenue_fn(train_data, -0.1, 0.1, 1, policy))
## give everyone -10% discount
policy_dic["Give Everyone Negative Discount"] = np.mean(revenue_fn(train_data, -0.1, 0, 1, np.ones(len(X))))
# get policy summary table
res = pd.DataFrame.from_dict(policy_dic, orient="index", columns=["Revenue"])
res["Rank"] = res["Revenue"].rank(ascending=False)
res
这里面的一顿操作有点费解的是,
intrp.treat(X)
这个输出的是什么: 每个人是否要进行打折,根据
SingleTreePolicyInterpreter
来判定,输出内容[0,1],这里的每个人指的是训练集的
X
,至于打多少折,这里默认为
0.1
里面还有一组很骚气的组,
Our Policy + Give Negative Discount for No-Discount Group
,竟然敢对不推荐给折扣的人涨价,当然revenue是上去的,rank排名第1。
输出结果:

3 智能营销案例二:(econml+dowhy)不同优惠折扣下的用户反应
是上面的案例【智能营销案例一:(econml)不同优惠折扣下的用户反应】的延申,一些数据计算过程都与上面一致,所以一些内容我就不赘述了。
链接:
类似的dowhy + econml的案例也可以看: -
-
3.1 背景
如【2.1】
3.2 数据准备与理解
如【2.2】
3.3 生成假的Groud Truth的估计效应
如【2.3】
3.4 利用dowhy创建因果图 + EconML创建线性估计器LinearDML
这里因为econml和dowhy集成非常好,所以可以非常好的无缝衔接与使用。 那么dowhy主要是需要发挥其因果图方面的能力。 通过定义这些假设,DoWhy可以为我们生成一个因果图,并使用该图首先识别因果效应。
# initiate an EconML cate estimator
est = LinearDML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor(),
featurizer=PolynomialFeatures(degree=2, include_bias=False))
# fit through dowhy
est_dw = est.dowhy.fit(Y, T, X=X, W=W, outcome_names=["log_demand"], treatment_names=["log_price"], feature_names=["income"],
confounder_names=confounder_names, inference="statsmodels")
# Visualize causal graph
# Try pretty printing the graph. Requires pydot and pygraphviz
display(
Image(to_pydot(est_dw._graph._graph).create_png())
except:
# Fall back on default graph view
est_dw.view_model()
LinearDML
是常规的econml的线性估计器,这里利用直接在估计器上再模拟一个因果图(
est.dowhy.fit
) 因果图这里就需要把,X/W/T都定义好,具体如下图:

构建了因果图,就可以探索变量之间,有没有更深层的关系(前门、后门、IV):
identified_estimand = est_dw.identified_estimand_
print(identified_estimand)输出如下:
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor1 (Default)
Estimand expression:
────────────(Expectation(log_demand|is_US,has_membership,days_visited,age,inco
d[log_price]
me,account_age,avg_hours,songs_purchased,friends_count))
Estimand assumption 1, Unconfoundedness: If U→{log_price} and U→log_demand then P(log_demand|log_price,is_US,has_membership,days_visited,age,income,account_age,avg_hours,songs_purchased,friends_count,U) = P(log_demand|log_price,is_US,has_membership,days_visited,age,income,account_age,avg_hours,songs_purchased,friends_count)
### Estimand : 2
Estimand name: iv
No such variable found!
### Estimand : 3
Estimand name: frontdoor
No such variable found!因为有定义混杂因子W,所以这里X -> Y,一般都是有后门路径的。 没有前门路径做阻断。
了解完变量之间的因果关系之后可以拿到具体的处理效应:
lineardml_estimate = est_dw.estimate_
print(lineardml_estimate)输出为:
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
────────────(Expectation(log_demand|songs_purchased,avg_hours,days_visited,has
d[log_price]
_membership,account_age,age,income,is_US,friends_count))
Estimand assumption 1, Unconfoundedness: If U→{log_price} and U→log_demand then P(log_demand|log_price,songs_purchased,avg_hours,days_visited,has_membership,account_age,age,income,is_US,friends_count,U) = P(log_demand|log_price,songs_purchased,avg_hours,days_visited,has_membership,account_age,age,income,is_US,friends_count)
## Realized estimand
b: log_demand~log_price+songs_purchased+avg_hours+days_visited+has_membership+account_age+age+income+is_US+friends_count | income
Target units: ate
## Estimate
Mean value: -0.997133982212133
Effect estimates: [-1.09399505 -1.48371714 -0.83401226 ... -1.3358834 -1.91959094
-0.40863328]
可以看到这里的CHTE的效应值为:
-0.997133982212133
这里的效应是什么意思? 这里的效应是T -> Y,T = 1 / T = 0 的情况下,demand=Y的变量 以及与后面估计值有啥差异? 后面的是Y~(X|T)的变化,这里也就是弹性了
估计弹性,这个部分与【2.4】线性估计内容一致
# Get treatment effect and its confidence interval
te_pred = est_dw.effect(X_test).flatten()
te_pred_interval = est_dw.effect_interval(X_test)
# Compare the estimate and the truth
plt.figure(figsize=(10, 6))
plt.plot(X_test.flatten(), te_pred, label="Sales Elasticity Prediction")
plt.plot(X_test.flatten(), truth_te_estimate, "--", label="True Elasticity")
plt.fill_between(
X_test.flatten(),
te_pred_interval[0].flatten(),
te_pred_interval[1].flatten(),
alpha=0.2,
label="95% Confidence Interval",
plt.fill_between(
X_test.flatten(),
truth_te_lower,
truth_te_upper,
alpha=0.2,
label="True Elasticity Range",
plt.xlabel("Income")
plt.ylabel("Songs Sales Elasticity")
plt.title("Songs Sales Elasticity vs Income")
plt.legend(loc="lower right")
3.5 EconML因果树估计器CausalForestDML + dowhy构建因果图
大部分与【2.5】一致,就是构造因果树估计器的同时,再额外构建因果图:
# initiate an EconML cate estimator
est_nonparam = CausalForestDML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor())
# fit through dowhy
est_nonparam_dw = est_nonparam.dowhy.fit(Y, T, X=X, W=W, outcome_names=["log_demand"], treatment_names=["log_price"],
feature_names=["income"], confounder_names=confounder_names, inference="blb")3.6 dowhy基于因果树的估计稳定性检验:反驳
具体可参考:
大致的一些反驳的方式
# Add Random Common Cause
res_random = est_nonparam_dw.refute_estimate(method_name="random_common_cause")
print(res_random)
# Add Unobserved Common Cause
res_unobserved = est_nonparam_dw.refute_estimate(
method_name="add_unobserved_common_cause",
confounders_effect_on_treatment="linear",
confounders_effect_on_outcome="linear",
effect_strength_on_treatment=0.1,
effect_strength_on_outcome=0.1,
print(res_unobserved)
#Replace Treatment with a Random (Placebo) Variable
res_placebo = est_nonparam_dw.refute_estimate(
method_name="placebo_treatment_refuter", placebo_type="permute",
num_simulations=3
print(res_placebo)
# Remove a Random Subset of the Data
res_subset = est_nonparam_dw.refute_estimate(
method_name="data_subset_refuter", subset_fraction=0.8,
num_simulations=3)
print(res_subset)3.7 T~X分析:SingleTreePolicyInterpreter 什么收入的人该打折
【如2.7】
3.8 干预后的结果对比(该打折的人打折后)
【如2.8】
4 案例:EconML + SHAP丰富可解释性
Interpretability with SHAP
类似于如何用SHAP解释黑箱预测机器学习模型,我们也可以解释黑箱效应异质性模型。这种方法解释了为什么异质因果效应模型对特定人群产生了较大或较小的效应值。是哪些特征导致了这种差异?
当模型被简洁地描述时,这个问题很容易解决,例如线性异质性模型的情况,人们可以简单地研究模型的系数。然而,当人们开始使用更具表现力的模型(如随机森林和因果森林)来建模效果异质性时,就会变得困难。SHAP值对于理解模型从训练数据中提取的影响异质性的主导因素有很大的帮助。 我们的软件包提供了与SHAP库的无缝集成。每个CateEstimator都有一个方法shap_values,它返回每个处理和结果对的估计器输出的SHAP值解释。
然后,可以使用SHAP库提供的大量可视化功能对这些值进行可视化。此外,只要有可能,我们的库就会为每种最终模型类型从SHAP库中调用快速专用算法,这可以大大减少计算时间。
4.1 单干预 - 单输出
## Ignore warnings
from econml.dml import CausalForestDML, LinearDML, NonParamDML
from econml.dr import DRLearner
from econml.metalearners import DomainAdaptationLearner, XLearner
from econml.iv.dr import LinearIntentToTreatDRIV
import numpy as np
import scipy.special
import matplotlib.pyplot as plt
import shap
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from sklearn.linear_model import Lasso
np.random.seed(123)
n_samples = 5000
n_features = 10
true_te = lambda X: (X[:, 0]>0) * X[:, 0]
X = np.random.normal(0, 1, size=(n_samples, n_features))
W = np.random.normal(0, 1, size=(n_samples, n_features))
T = np.random.binomial(1, scipy.special.expit(X[:, 0]))
y = true_te(X) * T + 5.0 * X[:, 0] + np.random.normal(0, .1, size=(n_samples,))
X_test = X[:min(100, n_samples)].copy()
X_test[:, 0] = np.linspace(np.percentile(X[:, 0], 1), np.percentile(X[:, 0], 99), min(100, n_samples))
# 因果树估计器
est = CausalForestDML(random_state=123)
est.fit(y, T, X=X, W=W)
# 线性估计器
est = LinearDML(random_state=123)
est.fit(y, T, X=X, W=W)
# 非参数
est = NonParamDML(model_y=RandomForestRegressor(min_samples_leaf=20, random_state=123),
model_t=RandomForestRegressor(min_samples_leaf=20, random_state=123),
model_final=RandomForestRegressor(min_samples_leaf=20, random_state=123),
random_state=123)
est.fit(y.ravel(), T.ravel(), X=X, W=W)
# 双重鲁棒学习
est = DRLearner(model_regression=RandomForestRegressor(min_samples_leaf=20, random_state=123),
model_propensity=RandomForestClassifier(min_samples_leaf=20, random_state=123),
model_final=RandomForestRegressor(min_samples_leaf=20, random_state=123),
random_state=123)
est.fit(y.ravel(), T.ravel(), X=X, W=W)
# 元学习 DomainAdaptationLearner
est = DomainAdaptationLearner(models=RandomForestRegressor(min_samples_leaf=20, random_state=123),
final_models=RandomForestRegressor(min_samples_leaf=20, random_state=123),
propensity_model=RandomForestClassifier(min_samples_leaf=20, random_state=123))
est.fit(y.ravel(), T.ravel(), X=X)
# Xlearner 元学习
# Xlearner.shap_values uses a slow shap exact explainer, as there is no well defined final model
# for the XLearner method.
est = XLearner(models=RandomForestRegressor(min_samples_leaf=20, random_state=123),
cate_models=RandomForestRegressor(min_samples_leaf=20, random_state=123),
propensity_model=RandomForestClassifier(min_samples_leaf=20, random_state=123))
est.fit(y.ravel(), T.ravel(), X=X)
# 工具变量
est = LinearIntentToTreatDRIV(model_y_xw=RandomForestRegressor(min_samples_leaf=20, random_state=123),
model_t_xwz=RandomForestClassifier(min_samples_leaf=20, random_state=123),
flexible_model_effect=RandomForestRegressor(min_samples_leaf=20, random_state=123),
random_state=123)
est.fit(y.ravel(), T.ravel(), Z=T.ravel(), X=X, W=W)输出一个图来看:
est = CausalForestDML(random_state=123)
est.fit(y, T, X=X, W=W)
shap_values = est.shap_values(X[:20])
shap.plots.beeswarm(shap_values['Y0']['T0'])详细的SHAP可参考:
特征密度散点图:beeswarm
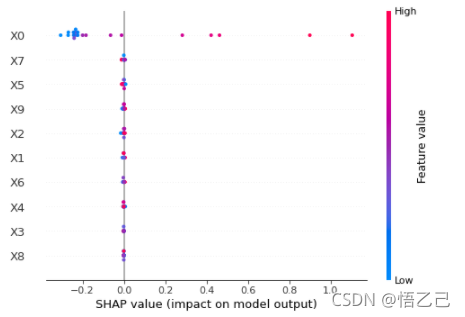
下图中每一行代表一个特征,横坐标为Shap值。特征的排序是按照shap 的平均绝对值,对模型来说的最重要特征。宽的地方表示有大量的样本聚集。
一个点代表一个样本,颜色越红说明特征本身数值越大,颜色越蓝说明特征本身数值越小。
可以看做一种特征重要性的排列图,从这里可以看到X0重要性高(排位); 同时,X0值越大,对模型的效果影响越好(SHAP值为正)
4.2 多干预 - 多输出
# 数据生成
np.random.seed(123)
n_samples = 5000
n_features = 10
n_treatments = 2
n_outputs = 3
true_te = lambda X: np.hstack([(X[:, [0]]>0) * X[:, [0]],
np.ones((X.shape[0], n_treatments - 1))*np.arange(1, n_treatments).reshape(1, -1)])
X = np.random.normal(0, 1, size=(n_samples, n_features))
W = np.random.normal(0, 1, size=(n_samples, n_features))
T = np.random.normal(0, 1, size=(n_samples, n_treatments))
for t in range(n_treatments):
T[:, t] = np.random.binomial(1, scipy.special.expit(X[:, 0]))
y = np.sum(true_te(X) * T, axis=1, keepdims=True) + 5.0 * X[:, [0]] + np.random.normal(0, .1, size=(n_samples, 1))
y = np.tile(y, (1, n_outputs))
for j in range(n_outputs):
y[:, j] = (j + 1) * y[:, j]
X_test = X[:min(100, n_samples)].copy()
X_test[:, 0] = np.linspace(np.percentile(X[:, 0], 1), np.percentile(X[:, 0], 99), min(100, n_samples))
est = CausalForestDML(n_estimators=400, random_state=123)
est.fit(y, T, X=X, W=W)
shap_values = est.shap_values(X[:200])
plt.figure(figsize=(25, 15))
for j in range(n_treatments):