定义:集合
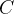 的仿射维数为其仿射包的维数。
的仿射维数为其仿射包的维数。
【通俗理解】
仿射包包含集合
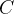 中任意点的线性组合。所有线性组合最终组成的空间是几维,仿射包就是几维。比如
中任意点的线性组合。所有线性组合最终组成的空间是几维,仿射包就是几维。比如
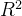 上的单位圆环,任意点的线性组合都在一个平面上,即单位圆环的仿射维数是2维。
上的单位圆环,任意点的线性组合都在一个平面上,即单位圆环的仿射维数是2维。
相对内部与相对边界
定义:若集合
 的仿射维数小于n(比如一个正方形在三维空间
的仿射维数小于n(比如一个正方形在三维空间
 内),那么集合
内),那么集合
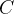 在仿射集合
在仿射集合
 中。我们称集合C的相对内部为
中。我们称集合C的相对内部为
 的内部,记为
的内部,记为
 。
。
数学表达:

其中
 , 即半径为r,中心为x并由
范数
|| ||定义的球。
, 即半径为r,中心为x并由
范数
|| ||定义的球。
举个简单的例子,比如集合C是一个正方形(二维图形),表达为
显然,它的仿射包就是
 对应的二维平面,表达为
对应的二维平面,表达为
现在要求集合
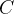 的相对内部,那就得先找
的相对内部,那就得先找
 ,它的形状是个球,有两个参数x和r。这里的x是在集合C里的,半径r的值可任意调整。可以想象,
,它的形状是个球,有两个参数x和r。这里的x是在集合C里的,半径r的值可任意调整。可以想象,
 其实就是球在
其实就是球在
 平面上的截面,形状是半径为r的圆形。
平面上的截面,形状是半径为r的圆形。
一个圆形所有点都要在集合C内,如果x取的是集合C的边界,比如
 ,那无论半径r取多小,都会存在圆形的某个点不在集合C内;而如果x取的是集合C内部的点
,那无论半径r取多小,都会存在圆形的某个点不在集合C内;而如果x取的是集合C内部的点
 ,那就不存在这个问题了。
,那就不存在这个问题了。
因此,集合C的相对内部为
定义:集合C的相对边界为
 ,
,
 表示C的闭包。
表示C的闭包。
【通俗理解】
简单理解就是,把集合C比作裱画,相对内部就是画像,画像的画框即为相对边界。相对边界一般为集合C取值范围的上下界。
什么是子空间?
这里的子空间指的是线性代数中的子空间,定义如下[1]:
设W为
数域
F上的n维线性空间V的子集合(即
 ),若W中的元素满足
),若W中的元素满足
(1)若
 ,则
,则
 ;(对加法是封闭的,即加法结果仍在集合W内)
;(对加法是封闭的,即加法结果仍在集合W内)
(2)若
 ,则
,则
 。(对数乘也是封闭的,即数乘结果仍在集合W内)
。(对数乘也是封闭的,即数乘结果仍在集合W内)
补充
:子空间中必须包含零向量(若
 ,则
,则
 )
)
易证W构成数域F上的线性空间。由
 得,W是线性空间V的一个线性子空间,简称子空间。
得,W是线性空间V的一个线性子空间,简称子空间。
子空间与仿射集合是什么关系?
1. 如果
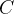 是一个仿射集合,且
是一个仿射集合,且
 ,则集合
,则集合
 ,是一个与仿射集合
,是一个与仿射集合
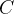 相关联的子空间[证明见注]。
相关联的子空间[证明见注]。
2. 定义仿射集合
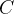 的维数为子空间
的维数为子空间
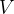 的维数,其中
的维数,其中
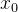 是
是
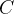 中的任意元素。
中的任意元素。
3. 直观理解:仿射集合与子空间的区别 (取自[2]的图),
子空间必过零点
[
注
] 证明:
设
 , 则有
, 则有
 .
.
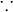 C 是仿射集合
C 是仿射集合
 满足子空间(1)(2)条件,证毕。
满足子空间(1)(2)条件,证毕。
范数
:举个例子,在二维的欧氏几何空间中定义欧氏范数。在该矢量空间中,元素被刻画为一个从原点出发,带有箭头的有向线段,每一个矢量的有向线段的长度即为该矢量的欧氏范数[3]。
数域:
设P是由一些复数组成的集合,其中包括0和1。若P中任意两个数的和、差、积、商(除数不为0)仍是P中的数,则称P为一个数域[4]。
[1]
子空间_百度百科
[2]
仿射集合与子空间的关系_Tomcat的专栏-CSDN博客
[3]
范数_百度百科
[4]
数域_百度百科
[美]S. Boyd, L. Vandenberghe. 凸优化[M]. 王书宁, 许鋆, 黄晓霖. 北京: 清华大学出版社, 2013.
前面讲了梯度下降的方法,关键在于步长的选择:固定步长、线搜索、BB方法等,但是如果优化函数本身存在不可导的点,就没有办法计算梯度了,这个时候就需要引入次梯度(Subgradient),这一节主要关注次梯度的计算。
1. 次梯度
次梯度(subgradient)的定义为
∂f(x)={g∣f(y)≥f(x)+gT(y−x),∀y∈domf}
\partial f(x)= \{g|f(y)\ge f(...
中的点,允许进行
仿射
组合(即系数和为1的线性组合)所能到达的所有点的集合。它可以被看作是“拉伸”中的一个平面),但在其
仿射
包(这个平面本身)内,它是有
内部
的。的
仿射
维度是其
仿射
包的维度,即。所“占据”
空间
的最小维度。以填满其所在的最小平面或
空间
。在整个
空间
中没有
内部
(例如在。在其
仿射
包内的
内部
。作为
仿射
空间
的维度。
根据定义,RnR^n中点x,yx,y之间的欧几里得距离是
d(x,y)=|x−y|=⟨x−y,x−y⟩1/2
d(x,y)=|x-y|=\langle x-y,x-y\rangle^{1/2}
函数dd(欧几里得度量)是R2nR^{2n}上的凸函数,(这个结论基于的事实是:将欧几里得范数f(z)=|z|f(z)=|z|和从R2nR^{2n}到RnR^n的线性变换(x,y)→x−y(x,y)\to