华泰金融工程研究组研报学习笔记——基于遗传规划的alpha因子挖掘

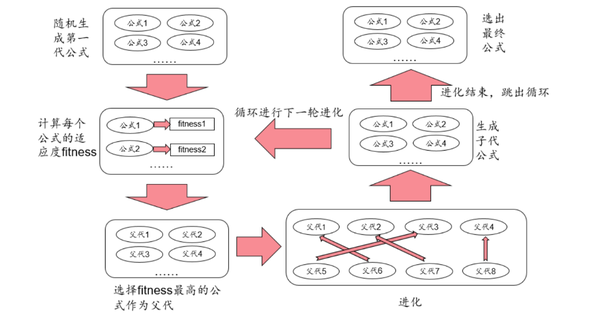
遗传规划的总体流程

遗传规划(genetic programming) 是演化算法(evolutionary algorithm)的分支，是一种启发式的公式演化技术。遗传规划从随机生成的公式群体开始，通过模拟自然界中遗传进化的过程，来逐渐 生成契合特定目标的公式群体 。

在量化多因子选股领域中， 因子的挖掘 是一个关注度经久不衰的主题：

• 以往的因子研究中，人们一般从市场可见的规律和投资经验入手，进行因子挖掘和改进，即“先有逻辑、后有公式”的方法，常见的因子如估值、成长、财务质量、波动率等都是通过这种方法研究得出的。
• 随着市场可用数据的增多和机器学习等先进技术的发展，我们可以借助遗传规划的方法在海量数据中进行探索，通过“进化”的方式得出一些经过检验有效的选股因子，再试图去解释这些因子的内涵，即“先有公式、后有逻辑”的方法。

以上两种方式对应于选股因子研究方法中的“演绎法”与“归纳法”，都有一定的存在基础。而后者的优势在于 可以充分利用计算机的强大算力进行启发式搜索，同时突破人类的思维局限，挖掘出某些隐藏的、难以通过人脑构建的因子 ，为因子研究提供更多的可能性。

遗传规划的流程图

程序结果如图：

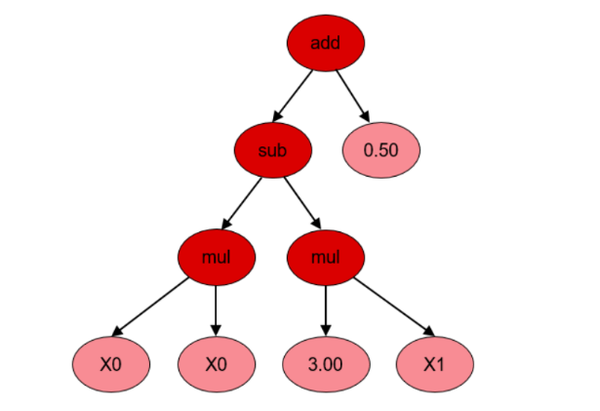
遗传规划中公式的表示方式

为了方便进行公式的进化，遗传规划中的公式一般会被表示成二叉树的形式，在这个二叉树里，所有的叶子都是变量或者常数，内部节点则是函数。树内的任意子树都可以被修改或替代。公式的输出值可以用递归的方法求得。（树的Length是树的节点的数量）

遗传规划中的适应度（fitness，由metric参数控制）

类比于自然界中个体对其生存环境的适应程度，在遗传规划中，每个公式也有自己的适应度，适应度衡量了公式运算结果与给定目标的相符程度，是公式进化的重要参考指标。

• 回归问题：均方误差 (y_pred - y_test)^2.mean()，平均绝对误差MAE
• 分类问题：交叉熵（分布之间的差异）
• 遗传规划生成因子：IC，RankIC，因子收益率

遗传规划中公式的进化方法

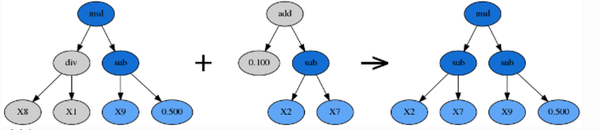
• 交叉（p_crossover参数控制）：
• 交叉是在两个已有公式树之间生成子树的方法，是最常用也最有效的进化方式。交叉需要通过两次选取找到父代和捐赠者
  

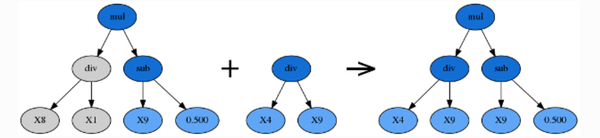
• 子树变异（p_subtree_mutation参数控制）
  子树变异是一种激进的变异操作，父代公式树的子树可以被完全随机生成的子树所取代。这可以将已被淘汰的公式重新引入公式种群，以维持公式多样性。
  

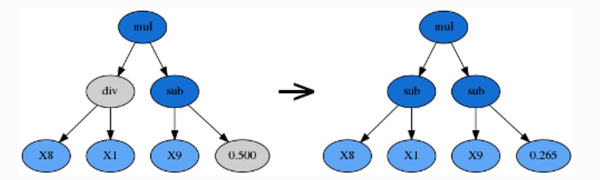
• 点变异（p_point_replace参数控制）
  点变异是另一种常见的变异形式。与子树变异一样，它也可以将已淘汰的公式重新引入种群中以维持公式多样性。
  

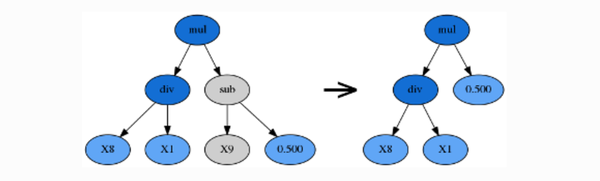
• Hoist变异（p_hoist_mutation参数控制）
  Hoist(提升)变异是一种对抗公式树过于复杂的方法。这种变异的目的是从公式树中移除部分叶子或者节点，以精简公式树。
  

遗传规划训练结果，new factor（自己编的example）：
>>> print(m1)

[mul(X1, 0.908),

mul(div(add(X4, X1), sub(X0, sub(X1, X0))), X2),

div(add(X1, X4), add(sub(X4, div(X1, sub(X1, X0))), sub(add(mul(X3, X3), X2), X4)))]

---

参考材料：

华泰金工研报：基于遗传规划的选股因子挖掘