分数量子霍尔效应笔记(一)---概要
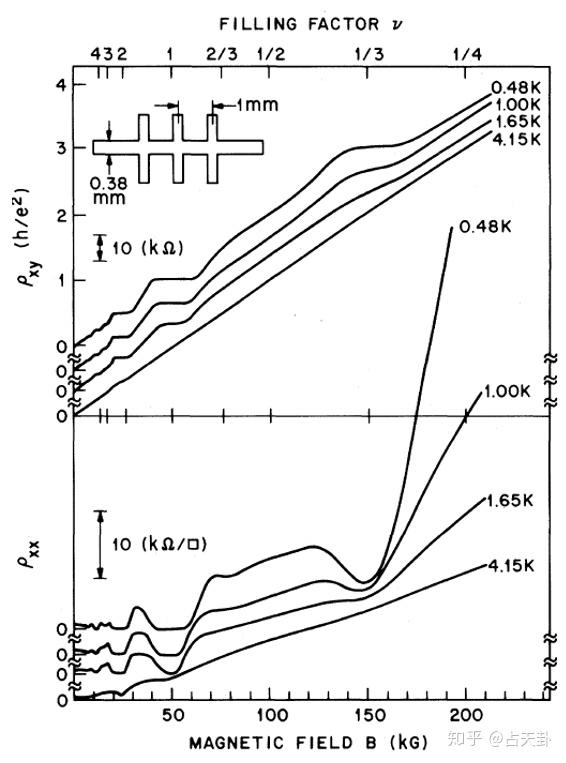
1982年,崔琦等人在MBE制备的GaAs/AlGaAs异质结二维电子气体中发现,在温度为0.48K,并且磁场加到15T时会出现一个新的量子霍尔态(纵向电阻降低为0,横向电阻出现平台)。由于此时的磁场恰好是最后一个整数量子霍尔效应的3倍,因此所对应的填充数为 \nu=\frac{1}{3} ,该效应也被称为分数量子霍尔效应。(填充数的定义为填满朗道能级的数量, 并且有关系: \nu=\frac{n_eh}{eB} 。)
1983年Laughlin猜出填充因子为1/m的波函数形式(m为奇数): \psi_{\frac{1}{m}}(z_i)=\prod_{i\ne j}(z_i-z_j)^me^{-\frac{1}{4l_B^2}\sum_i|z_i|^2} 。
其中m对应角动量量子数,当m为奇数时,这个波函数满足交换反对称性,对应费米子;当m为偶数时,波函数满足交换对称性,对应玻色子。当i=j时,波函数为0,体现了泡利不相容原理。
该模型成功地解释了1/m量子霍尔态,但是无法解释更为一般的分数量子霍尔态。
1983年, Haldane和Halperin提出了阶层模型理论(HH model)用于解释更为一般的奇数分母的FQHE。
这种理论认为,当分数化的填充数变化的时候,就产生了一种“Laughlin quasiparticle”(LQP) ,这种LQP被视作一种有效磁通为 N\Phi_0 的玻色子。当LQP之间不发生相互作用时就不会产生新的不可压缩态,而当LQP之间(1)存在短程的互斥作用;(2)作用远弱于母态能隙时,就会在 \nu=\frac{1}{m\pm\frac{1}{q}} 时产生Laughlin-like的 FQHE态来制造新的不可压缩子态,其中 \frac{1}{q}=\frac{N_{LQP}}{N} (q为偶数)代表了LQP占总电子数的比例。而当LQP的LQP存在合适的相互作用时,会产生类似的子态的子态。最终在第n代的时给出填充数:
\nu=\frac{1}{m\pm\frac{1}{q_1\pm\frac{1}{q_3\pm\frac{1}{\cdots\pm \frac{1}{q_n}}}}}
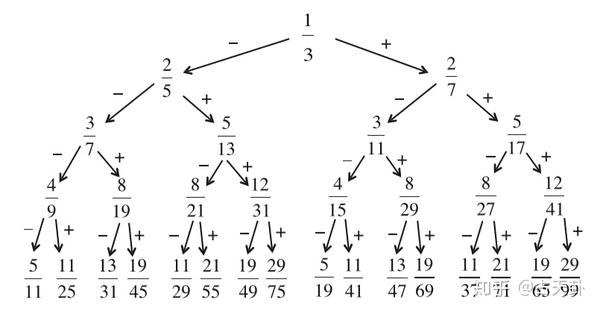
设LQP坐标为: \bm{\eta}=(\eta_x,\eta_y)=\eta_x+i\eta_y , \bm{r}=(x,y)=x+iy ,则对于 \nu>1/m 的第一个子态的HH波函数可以被写为:
\Psi_{\nu>\frac{1}{m}}=\int\prod_{\mu=1}^{N/q}d^2\bm{\eta}_\mu \bar\Phi_{1/q}(\bm{\eta}_\mu)\Psi_{1/m}^{LQP}(\bm{r}_j;\bm{\eta}_\mu)
其中
\Phi_{1/q}(\bm{\eta}_\mu)=\prod_{\mu<\nu}(\eta_\mu-\eta_\nu)^q ,
\Psi_{1/m}^{LQP}=\prod_{j=1}^{N}\prod_{\mu=1}^{N_{LQP}}(2\frac{\partial}{\partial r_j}-\bar\eta_\mu)\Phi_{1/m} 为位于 \left\{ \bm{\eta}_\mu\right\} 的 LQP的波函数。
对于 \nu<1/m 的第一个子态,只需要把LQP波函数改成相应的准空穴波函数:
\Psi_{1/m}^{LQP}=\prod_{j=1}^{N}\prod_{\mu=1}^{N_{LQH}}(r_j-\bar\eta_\mu)\Phi_{1/m}
1989年,Jain提出了复合费米子理论,引入了复合费米子(Comosite Fermion,简称CF)的概念。每个复合费米子由一个电子携带2p个量子磁通 \Phi_0 =h/e 组成。这种复合费米子感受到去除了 2pn_e\Phi_0 的有效磁场 B^*=B-2pn_e\Phi_0 ,形成它自己的“Landau能级”,为了与电子的朗道能级相区分,之后将称其为Lambda能级。
这种理论认为,所谓分数量子霍尔效应就是这种复合 \nu^*=1 费米子填充Lambda能级形成有效的整数量子霍尔效应。因此复合费米子的填充数 \nu 与实际上电子的填充数 \nu^* 应当满足关系:
\nu^*=\frac{n_eh}{e|B^*|}=\pm\frac{n_eh/eB}{1-2pn_eh/eB}=\pm\frac{\nu}{1-2p\nu} 。
也就是 \nu=\frac{\nu^*}{2p\nu^*\pm1} 。例如,对于1/3FQHE,每个复合费米子携带两个量子磁通(p=1),占据第一个Lamba能级( \nu^*=1 )。
此外,我们还可以得到有效磁场和原磁场的关系:
|B^*|=|B-2pn_eh/e|=|1-2p\nu|B=\frac{\nu}{\nu^*}B=\frac{1}{2p\nu^*\pm1}B
以及处于第一朗道能级内的复合费米子的相互作用强度应当为库伦相互作用的形式:
\hbar\omega_c^*=\frac{\hbar e|B^*|}{m^*}=\frac{1}{2p\nu^*\pm1}\frac{eB\hbar}{m^*}\sim\frac{1}{2p\nu^*\pm1}\frac{e^2}{\epsilon l_B}
其中 l_B=\sqrt{\frac{\hbar}{eB}} 为磁长度, \epsilon 为介电常数。可以看到有效质量应当满足 m^*\sim\sqrt{B} 的形式。
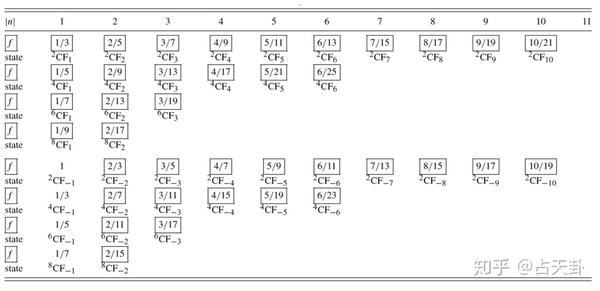
Read等人提出,对于 \nu^*\rightarrow\infty 的情形,有 B^*\rightarrow0 , \nu\rightarrow\frac{1}{2p} 。被称为这种复合费米子的费米海。
按照这种理论构建出的基态波函数为:
\Psi_{\nu=\nu^*/(2p\nu^*+1)}^{gs}=\Psi^{gs}_{\nu^*=n}=P_{LLL}\Phi^{CF,gs}_{\nu^*=n}\prod_{j<k}(r_j-r_k)^{2p}
其中,
\Phi^{gs}_{\nu^*=n}
是电子在第n个朗道能级的波函数,
\prod_{j<k}(r_j-r_k)^{2p}
为每个电子加上2p个量子磁通成为复合费米子的波函数 ,
P_{LLL}
将复合费米子波函数投影到第一个Lambda能级上。
特别地,当n=1时,这个波函数将回到Laughlin波函数。
虽然说两种理论都给出了相同的准粒子电荷以及编织统计性质,并且在Chern-Simons理论中拥有等效的K矩阵,但是它们归根结底还是不一样的东西,并且在实验上给出了不同的预言:
1、对于1/m态的单粒子,这两种模型分别给出波函数:
\Psi^{LQP}=e^{-\sum_j\frac{|r_j|^2}{4}}\prod_l2\frac{\partial}{\partial r_l}\prod_{j<k}(r_j-r_k)^m
\Psi^{CF-QP}=e^{-\sum_j\frac{|r_j|^2}{4}}P_{LLL} \left|\begin{array}\bar{z_1}&\bar z_2&\cdots\\ 1&1&\cdots\\ z_1&z_2&\cdots\\ \vdots&\vdots&\vdots\\ z_1^{N-2}&z_2^{N-2}&\cdots \end{array}\right|\prod_{j<k}(r_j-r_k)^{2p} ,其中投影算符 P_{LLL} 是将行列式中的 \bar z_j 替换为了 2\frac{\partial}{\partial z_j} 。
可以看到,这两个波函数并不相同。计算库伦相互作后可以得到CF波函数的能量要比LQP波函数低上15%。
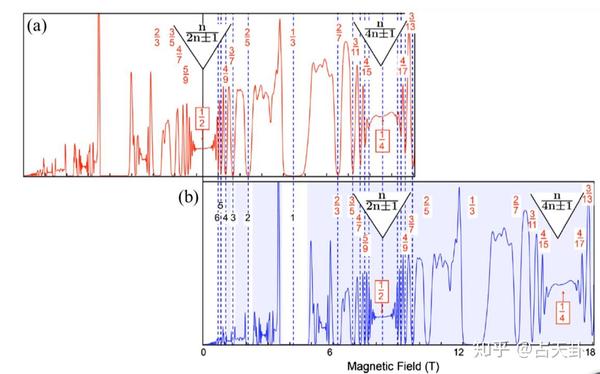
2、两种理论对于显著分数态给出了不同的预言。
由于LQP理论的模型要求准粒子相互作用远小于母态能隙,因此可以预见随着分数态一代一代往下迭代,能隙将会很快衰减。也就是说实验上能观测到的分数态应嘎爱爱主要集中在前几代之中。
类似地,CF理论中复合费米子本身产生的分数态也比较难被观测到,基本上只能观测到复合费米子的整数态及一些剩余作用引起的额外分数态。
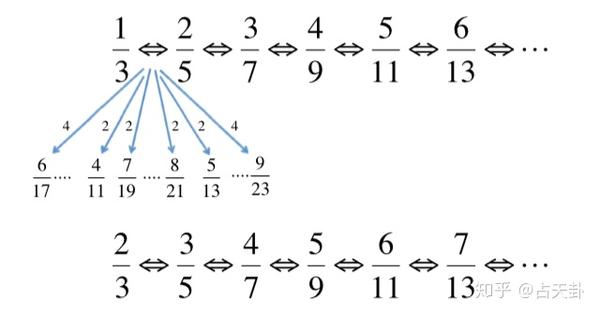
以6/13态为例。在CF理论中它可以由 \frac{6}{13}=\frac{6}{2\times1\times6+1} 产生,因此处于p=1(即一个复合费米子携带两个量子磁通)的第6个能级,是比较显著的。
而在HH理论中它需要沿着 \frac{1}{3}\rightarrow\frac{2}{5}\rightarrow\frac{3}{7}\rightarrow\frac{4}{9}\rightarrow\frac{5}{11}\rightarrow\frac{6}{13} 的途径产生,属于第六代子态,因此应当在实验上观察不到如此高阶的分数态信号。
3、费米海
HH理论当中无法在1/2p态处给出费米海的现象,而CF理论给出了这样的预言。
4、自旋极化
CF理论中预言了未充分自旋极化的FQHE,而HH理论中不包含这点。
从现有的实验证据上来看,以上四点都被验证是更加支持CF理论的。


