矩阵计算（一）：基础数值算法

海怡皮皮虾

世间安得双全法，不负如来不负卿

什么是矩阵的数值计算方法？

矩阵计算都是建立在线性代数运算的层次之上的，例如 点积（Dot Product） 涉及加法和乘法的标量运算， 矩阵向量乘法（Matrix-Vector Multiplication） 由点积组成， 矩阵-矩阵乘法（Matrix-Matrix Multiplication） 相当于矩阵-向量乘积的集合。所有这些操作都可以用算法的形式或线性代数的语言来描述。

本文的主要目的是介绍几种常见矩阵运算过程的数值计算形式，这种方式是从计算机计算角度去看整个过程，更重视计算的复杂程度。

几种基础且常见矩阵运算的数值算法

点积（Dot Product）

两个向量的点积就是分别把两个向量的对应元素相乘然后求和，举个例子：

a= \begin{bmatrix} 1\quad2 \end{bmatrix}^{T} ， b= \begin{bmatrix} 3\quad4 \end{bmatrix}^{T} ，则 a^{T}b= \begin{bmatrix} 1&2\\ \end{bmatrix} \begin{bmatrix} 3\\4 \end{bmatrix} =1\times3+2\times4=11

在计算机中，如果有向量 x、y\in R^{n} ，那么它们俩点积 c=x^{T} y 的计算方式如下：

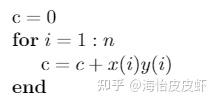
从上图的算法中可以清楚地看出，两个 n 维向量的点积包括 n 次乘法和 n 次加法，省去常数项以后，可得点积运算的计算复杂度为 O(n) ，这表明点积的计算复杂度与向量的规模大小成正比。

外积（Outer Product）

两个向量的外积和两个向量的内积过程是相反的，内积的过程会使向量的维度降低，而外积则是一个升维操作，举个例子：

\begin{bmatrix} 1\\2\\ 3\end{bmatrix} \begin{bmatrix} 4&5 \end{bmatrix}=\begin{bmatrix} 4&5\\ 8&10\\ 12&15 \end{bmatrix}

本来的两个向量都是一维向量，经过外积操作以后，变成了一个二维矩阵。外积具体的物理意义往后会有文章进行专门的讲解，这里我们还是主要关注其计算过程。

如果 A\in R^{m\times n} ， x\in R^{m} ， y\in R^{n} ，那么两个向量的外积 A=x y^{T} 算法如下：

整个过程经历了 m\times n 次循环过程，其算法复杂度为 O(mn) 。

矩阵向量乘法（Matrix-Vector Multiplication）

矩阵和向量的乘法可以从两个角度去看。一是看作是由多个向量的点积操作的集合；二是可以看成矩阵列的线性组合。

点积操作的集合

说矩阵与向量乘积是点积操作集合的原因是，在这个过程中每一步都在进行着点积的操作，先看个例子：

\begin{bmatrix} 1&2\\ 3&4\\ 5&6 \end{bmatrix} \begin{bmatrix} 7\\8 \end{bmatrix}= \begin{bmatrix} 1\times7+2\times8\\ 3\times7+4\times8\\ 5\times7+6\times8 \end{bmatrix} =\begin{bmatrix} 23\\53\\83 \end{bmatrix}

这个例子中，一共进行了三次点积的操作，分别是 \begin{bmatrix} 1&2\\ \end{bmatrix} \begin{bmatrix} 7\\8 \end{bmatrix} 、 \begin{bmatrix} 3&4\\ \end{bmatrix} \begin{bmatrix} 7\\8 \end{bmatrix} 和 \begin{bmatrix} 5&6\\ \end{bmatrix} \begin{bmatrix} 7\\8 \end{bmatrix} ，所以我们称它是点积操作的集合。

如果有矩阵 A\in R^{m\times n} ，向量 x\in R^{n} ，那么矩阵和向量的乘积 y=Ax 计算方式如下：

显而易见，该算法的复杂度为 O(mn) ，因为它需要对矩阵的每一行都进行一次点积操作。

矩阵列的线性组合

现在我们用另一种角度去看矩阵和向量积的运算，还是刚才那个例子，我们可以换种计算方式，例如：

\begin{bmatrix} 1&2\\ 3&4\\ 5&6 \end{bmatrix} \begin{bmatrix} 7\\8 \end{bmatrix}= 7\times\begin{bmatrix} 1\\ 3\\ 5\end{bmatrix}+8\times\begin{bmatrix}2\\4\\6\end{bmatrix} =\begin{bmatrix} 23\\53\\83 \end{bmatrix}

这种方式就是矩阵列的线性组合。它其实是一种分解的思想，在后面的矩阵乘法中还会见到类似的分解。当然，后续我们也会对这种做法的物理意义进行探讨。接下来同样来看一下这个过程的计算方法：

利用矩阵列的线性组合的形式去计算矩阵向量的乘积，只是换了一种角度去看待这个问题，但算法复杂度并没有发生改变，依然是 O(mn) 。

矩阵-矩阵乘法（Matrix-Matrix Multiplication）

在上面的介绍中，我们主要介绍了三种不同的形式：内积、外积和 列的线性组合 。接下来，我们把这三种形式应用到矩阵乘法上，从不同角度去看矩阵乘法。

内积角度

从内积的角度看矩阵乘法，其实就是说新矩阵的每一个元素都是由内积操作得到的：

\begin{bmatrix} 1&2\\ 3&4\end{bmatrix} \begin{bmatrix} 5&6\\ 7&8\end{bmatrix} = \begin{bmatrix} 1\times 5+2\times7&1\times6+2\times8\\ 3\times 5+4\times7&3\times6+4\times8\end{bmatrix}

整个矩阵计算的过程其实就是计算 \begin{bmatrix} 1&2\\ \end{bmatrix} \begin{bmatrix} 5\\7 \end{bmatrix} 、 \begin{bmatrix} 1&2\\ \end{bmatrix} \begin{bmatrix} 6\\8 \end{bmatrix} 、 \begin{bmatrix} 3&4\\ \end{bmatrix} \begin{bmatrix} 5\\7 \end{bmatrix} 、 \begin{bmatrix} 3&4\\ \end{bmatrix} \begin{bmatrix} 6\\8 \end{bmatrix} 这四个内积。

外积角度

向量的外积运算在前文有过介绍，这里我们直接给出矩阵乘法的外积形式：

\begin{bmatrix} 1&2\\ 3&4\end{bmatrix} \begin{bmatrix} 5&6\\ 7&8\end{bmatrix} =\begin{bmatrix} 1\\ 3\end{bmatrix}\begin{bmatrix} 5&6\end{bmatrix}+ \begin{bmatrix} 2\\ 4\end{bmatrix}\begin{bmatrix} 7&8\end{bmatrix}\

这种正向的过程并不是外积带给我们的最大好处，相反逆向的过程对我们的启发更大，它在 矩阵分解 中发挥着重要的作用。

列的线性组合角度

在这个视角中，新矩阵的每一列都被看作是一个线性组合的形式：

\begin{bmatrix} 1&2\\ 3&4\end{bmatrix} \begin{bmatrix} 5&6\\ 7&8\end{bmatrix} =\begin{bmatrix} 5\begin{bmatrix} 1\\ 3\end{bmatrix}+7\begin{bmatrix} 2\\ 4\end{bmatrix}， 6\begin{bmatrix} 1\\ 3\end{bmatrix}+8\begin{bmatrix} 2\\ 4\end{bmatrix}\end{bmatrix}

看完了矩阵乘法的三种形式，接下来我们还是去关注一下具体的计算过程。

如果有矩阵 A\in R^{m\times r} 、 B\in R^{ r\times n} 、 C\in R^{m\times n} 且 C 为零矩阵，那么矩阵 C=AB 计算过程如下：