《运筹学导论》总结
本文章主要总结课程《运筹学导论》,可以让读者大致了解运筹学的基本知识,以及运用的方法。
绪论
什么是运筹学
给定目标和条件->选择最优方案->最优化技术
作用;
1.辅助决策
2.提高决策效率
3.优化决策效果
又称“又要马儿跑,又要马儿不吃草。”
怎么学运筹学
目标-影响因素分析-确定类型-选择理论与方法-分析与设计-决策
1.凝练问题
2.注重思维
3.培养能力
4.开阔视野
先修课程:
高等数学、线性代数、概率与数理统计
学习方式:
实际联系、课堂听课、分组讨论、联系实际
运筹学学什么
线性规划、排队论、动态规划、图与网络分析、对策论、非线性规划(储存论、决策论)
总结
什么是运筹学:最优化
怎么学运筹学:重思维
运筹学学什么:有点多
线性规划
问题:是得过且过,还是宁缺毋滥?
线性规划模型与求解
线性规划问题:
生产计划
输运方案
合理下料
配料问题
生产布局
合理利用
有限资源
,得到
最大
效益
线性规划模型三要素
1.决策变量 需决策的量
2.目标函数 需优化的量,即与达到的目标
3.约束条件 为实现优化目标受到的限制
线性规划数学模型一般形式
以极大型、小于等于为例
决策变量
x_1,...,x_n
目标函数
max z=c_1x_1+...+c_nx_n
约束条件
a_{11}x_1+...+a_{1n}x_n \leq b_1
...
a_{m1}x_1+...+a_{mn}x_n \leq b_m
x_1,...x_n \ge 0
二维线性规划问题特殊解法:图解法
1.做约束条件图形
2.做目标函数图形
3.求出最优解
可行解 满足全体约束的解,记为
X
最优解 可行解在最优的,记为
X^*
可行解是可行域中的
点
,是可行方案
最优解是可行域的
角点
,是最优方案
解的类型:
1.唯一解
2.多重最优解
3.无解
4.无有限最优解
线性规划问题的一般解法 :单纯形法

总结
1.线性规划三要素
决策变量、目标函数、约束条件
2.二维线性规划问题特殊解法-图解法
约束图形-目标图形-求最优解
3.线性规划问题一般解法-单纯形法
初始解-检验解-最优解
拓展
1.线性规划的对偶问题
对偶问题模型、性质、经济解释
2.线性规划的灵敏度分析
参数变化影响解的可行性/最优性
3.运输问题的表上作业法
最小元素法、伏格尔法、闭回路法、位势法
0-1整数规划
问题:To be or not to be?
0-1 整数规划数学模型
决策变量
x_i
—是否做第
i
件事
i=1,2...,n
x_i=\delta(x-i)
常见的几种约束条件
n件事中至少做k件事——
x_1+x_2+...+x_n \ge k
n件事中必须做k件并只能做k件事——
x_1+x_2+...+x_n=k
只在做了第i件事前提下才考虑是否做第j件事——
x_j \le x_i
n件事中最多做k件事——
x_1+x_2+...+x_n \le k
做第j件事的充要条件是做第j件事——
x_i=x_j
做第i件事的充要条件是不做第j件事——
x_i=1-x_j
背包问题
例子 一名旅行者在准备行装,最多携带总重量b,假设物品只能整件携带,每件物品规定“价值”, 共有n件物品可选,第i件物品重量为
b_i
,价值为
c_i
,则携带哪些物品可使总价值最大?
决策变量
x_i=\delta(x-i)
,i:带第i件物品
目标函数
max z=\sum_{i=1}^\infty c_ix_i
\sum_{i=1}^\infty b_ix_i \le b
x_i=0,1
i=1,...,n
指派问题
m=n
n项工作,由n个人承担
每项工作只由一人承担
每个人只承担一项工作
c_{ij}
:第i人做第j项工作费用
求总费用最低的方案

x_{ij}=\delta(i-j)
max z=\sum_j \sum_i c_ij x_ij
x_{i1}+x_{i2}+...+x_{ij}+...+x_{in}=1 i=1,2,...,n 每个人有事做
x_{1j}+x_{2j}+...+x_{ij}+...+x_{nj}=1 j=1,2,...,n 每件事有人做
x_{ij}=0,1
人数与工作数不等的指派问题
m<n
n项工作,由m个人承担
每项工作只由一人承担
每个人只承担一项工作
c_{ij}
:第i人做第j项工作费用
求总费用最低的方案

m>n
m项工作,由n个人承担
每项工作只由一人承担
每个人只承担一项工作
c_{ij}
:第i人做第j项工作费用
求总费用最低的方案

一个人可做几件事的指派问题
设m个人中的第k个人可同时做r件事, 第k个人视为r个人 (t个人做同一件事费用系数相等)

某人一定不能做某事的指派问题
min 问题——>第k个人一定不能做第t件事——>费用系数 c_{kt} 充分大
max 问题——>第k个人一定不能做第t件事——>费用系数 c_{kt} 充分小
总结
1.0-1整数规划数学模型
0-1变量
2.0-1整数规划建模
投资/背包/选址/固定费用/指派
延伸
1.整数规划解法
割平面法、分支定界法
2.指派问题解法
匈牙利算法、最大化问题转化
目标规划
问题:小孩子才做选择,成年人当然是全都要?
多目标问题:
决策者有若干目标值,实现目标有先后顺序
目标规划:
在给定资源条件下,求偏离目标值最小的方案
目标规划模型构成
偏差变量
正偏差变量:第i个目标的决策值 超出 其目标值部分,记作 d_i^+
负偏差变量:第i个目标的决策值 不足 其目标值部分,记作 d_i^-
三种情况:
(1)决策值超过目标值
d_i^+>0,d_i^-=0
(2)决策值等于目标值
d_i^+=d_i^-=0
(3)决策值未达目标值
d_i^+
=0,
d_i^-
<0
注意
d_i^+
,
d_i^-
至少一个为零,所以
d_i^+*d_i^-=0
目标函数
为达到目标要求的指标值,应使
d_i^+
,
d_i^-
尽可能小
三种情况:
(1)超过目标值
min z
=
f(d_i^-)
(2)等于目标值
min z
=
f(d_i^-,d_i^+)
(3)决策值未达目标值
min z
=
f(d_i^+)
eg:
min z
=
d_1^-
+
d_2^+
+
d_2^-
+
d_2^+
优先因子与权系数
优先因子 p_k :表达不同目标的重要性度
p_1\gg p_2\gg ...\gg P_n
权系数 \omega _j ;区分在同一优先级别中不同目标的重要程度(数字), 数字越大表明该目标越重要
绝对约束与目标约束
绝对约束
:必须严格满足的等式约束和不等式约束
目标约束
达到此目标值时允许发生正或负偏差,将约束条件右端项视为追求的目标值
目标函数+偏差变量——>目标约束
绝对约束+偏差变量——>目标约束
eg.产品对原料单耗不变,原料可补给,求总产值为2000万元及A产品产量为400吨的生产计划,A产量要先达到要求,其次考虑产值。
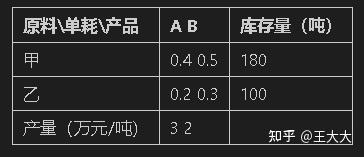
min z=p_2 (d_1^++d_1^-)+p_1 (d_2^++d_2^-)
3 x_1+2 x_2+d_1^--d_1^+=2000
x_1
+
d_2^-
-
d_2^+
=400
0.4
x_1
+0.5
x_2
\le
180
0.2
x_1
+0.3
x_2
\le
100
x_1,x_2,d_i^-,d_i^+ \geq 0,i=1,2
目标规划数学模型
目标函数: min z=\sum_{l=1}^L p_l \sum_{k=1}^K (\omega_{ik}^-d_k^- +\omega_{ik}^+d_k^+)
目标约束: \sum_{i=1}^n c_{ki}x_i+d_k^- -d_k^+=g_k,k=1,...,K
最对约束: \sum_{i=1}^n a_{ij}x_i \le(=,\ge)b_j,j=1,...,m
非负约束: x_i\ge0,i=1,...n d_k^+,d_k^-\ge0,k=1,...,K
eg.某工厂生产A、B两种产品,有关数据如下表。若资源可补充, 且A、B计划产量分别是4、5.确定一个生产方案,依次满足目标要求。
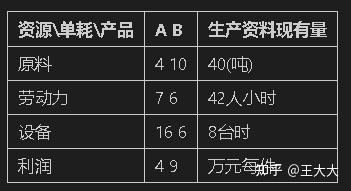
p_1 :产品数量不得超过计划指标
p_2 :加班时间最少
p_3 :利润达到最高指标
p_4 :设备利用率不超过最高指标
min z =p_1(d_1^++d_2^+)+p_2 d_3^++p_3 d_4^- + p_4 d_5^+
x_1 + d_1^- - d_1^+ =4
x_2
+
d_2^-
-
d_2^+
=5
6
x_2
+7
x_1
+
d_3^-
-
d_3^+
=42
4
x_1
+9
x_2
+
d_4^-
-
d_4^+
=61
16
x_1
+7
x_2
+
d_5^-
-
d_5^+
=80
4
x_1
+10
x_2
+
d_6^-
-
d_6^+
=40
x_1,x_2,d_i^-,d_i^+\ge0 i=1,...,6
总结
1.偏差变量
正偏差、负偏差
2.目标函数
标函数,min、优先因子、权系数
3.绝对约束与目标约束
硬/软约束、绝对约束可转目标约束
延申
目标规划解法: 图解法、单纯形法
动态规划
问题:是今朝有酒今朝醉还是放眼未来好期待?
多阶段决策问题
前后关联+链状结构+多阶段过=多过程决策过程
目标 寻找全过程最优方案
最短路问题
基本概念
阶段变量k: 原问题分成若干相互联系的子问题
状态变量
s_k
: 每阶段初可能的情形或位置
无后效性!
决策变量
x_k
(s): 每阶段状态确定后的抉择,即从该状态演变到下阶段某状态的选择
决策集合
D_k
(
s_k
)
状态转移: 由
s_k
转变为
s_{k+1}
的规律
s_{k+1}=T_k(s_k,x_k)
状态→决策→状态……
决策序列在变化的状态中产生
后部子策略
P_{k,n}(s_k)
: 阶段k至n的决策组成的序列{
x_k(s_k).….x_n(s_n)
}
策略
P_{i,n}(s_1)
阶段指标
v_k=v_k(s_k,x_k)
:
k阶段状态下选定决策
x_k
后产生的效益
动态规划最优解?
最优策略
P_{1,n}^*(s_1)
动态规划最优值?
最优指标函数
f_1(s_1)
基本方程
f_k(s_k) =opt{ v_k(s_k,x_k)+f_{k+1}(s_{k+1}) }
f_{n+1}(s_n+1) =0 k=n,...,1
动态规划求解步骤
确定过程分段构造状态变量——》设置决策变量写出状态转移——》列出阶段指标列出指标函数——》写出基本方程逐段递推求解
最优化原理
Bellman最优性原理:如果 P_{1,n}^*(s_1) 是最优策略,则对任意阶段k(1 是以s为起点的k至n子过程的最优策略
总结
1.多阶段决策问题
前后关联+链状+多阶段过程
2动态规划基本概念
阶段变量+决策变量+状态变量+状态转移+后部子策略+阶段指标+指标函数+最优指标函数
3.基本方程
f_k(s_k) =opt{ v_k(s_k,x_k)+f_{k+1}(s_{k+1}) }
f_{n+1}(s_n+1) =0 k=n,...,1
延申
1.动态规划应用
机器负荷、资源分配、设备更新、系统可靠性、背包问题、生产计划、不确定性采购.…
2.状态变量取值及定义
离散型、连续型、定义阶段初/末?
3.动态规划顺序解法
f_k(s_k) =opt{ v_k(s_k,x_k)+f_{k-1}(s_{k-1}) }
f_{0}(s_0) =0 k=n,...,1
图与最小支撑树
问题:是盘根错节有水平,还是大而化简显实力?
图
点(研究对象)+连线(研究对象的关系)=图
无向图
点(研究对象)+边( [v_i,v_j],[v_j,v_i] )=无向图( G=(V,E) )
有向图
点(研究对象)+弧( (v_i,v_j) )=有向图( G=(V,A) )
简单图和多重图
环:边的两个端点相同
多重边:两个端点之间有两条以上的边
简单图:无环无多重边的图
多重图:一个无环、有多重边的图
网络
有向图/无向图+权( w_{ij} )=网络
度
以点为端点的边的个数,记d(v)
弧立点:度为零的点
悬挂点:度为1的点
悬挂边:悬挂点的关联边
奇点:度为奇数的点
偶点:度为偶数的点
定理1
:所有顶点度数之和等于所有边数的2倍
定理2
:在任一图中,奇点的个数必为偶数
次
点
v_i
出次
d^+(v_i)
:以
v_i
为始点的边数点
点
v_I
入次
d^-(v_i)
:以
v_i
为终点的边数次
次=出次和入次之和
所有顶点的入次之和=所有顶点的出次之和
支撑子图
G_1=(V_1,E_1)
G_2=(V_2,E_2)
V_2 \subseteq V_1,E_2 \subseteq E_1 ——》 G_2 是 G_1 的子图
V_2=V_1,E_2 \subseteq E_1 ——》 G_2 是 G_1 的支撑子图
链、连通图与路
链
:由两两相邻的点及其相关联的边构成的
点边
序列
简单链:链中所含的
边
均不相同
初等链:所含的
点
均不相同
圈:
起点和终点
相重合的链
连通图
:图中任意两点之间均至少有一条链
路
:
v_{i1},a_{i1},v_{i2},a_{i2},...,v_{i,k-1},a_{i,k-1},v_{i,k},a_{i,k})
链中所有弧皆有 a_{i,t}=(v_{i,t},v_{i,t+1}),t=1,2,...,k
回路 :起点和终点重合的路
图的矩阵表示
权矩阵 a_{ij}=w_{ij}\delta(x-(v_i,v_j))
邻接矩阵: a_{ij}=\delta(x-(v_i,v_j))
(v_i,v_j) \subset E
树的概念和性质
无圈+连通+图=树
树:使图保持
连通
具有
最少边数
的图形
树的性质:
(1)树中任两点中有且仅有一条链
(2)树任删去一边则不连通
(3)边数=顶点数-1
图的支撑树
G=(V,E) 支撑子图 T=(V,E) 构成树,T为G的支撑树
最小支撑树
求赋权图的支撑树,使其边的 权和最小
避圈法
按权值 从小到大 填边——》若出现圈删权值 最大 边——》填 满 n-1条边(n为顶点数)
破圈法
在图中找 圈 ——》删除 权值最大 边——》图中 无圈
案例
某公司拟铺设海上油管,要求将海上六口油井连通,仅1号油井与海岸相连,距离为5海里。已知,海上六口油井间的距离如下表1。试问,应如何铺设油管使铺设油管的总长最短?
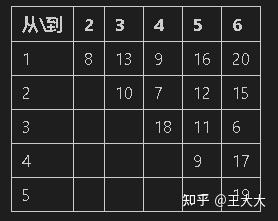
解答 海岸-1-2(-3-6)-4-5
总结
点+连线=图
树的定义
树的性质
图的支撑树
最小支撑树:求赋权图的支撑树,使其边的权和最小
解法:避圈法、破圈法
最短路
问题:是条条大道通罗马,还是终南捷径好通达?
用最短路给出
最短/省/方案
最短路
:
D=(V,A)
为连通图,求一条路
\mu
从起点
v_1
到终点
v_n
所有路中总权值最小
最短路问题算法(
w_ij
≥0)
Dijkstra基本思想:最短路的子路一定还是最短路
(
\alpha,\beta
)
\alpha:v_i 到当前点的最短路长
\beta
:最短路长中当前点的前接点
反向追踪
\beta
值得最短路
总结
1.最短路问题
多阶段、距离、成本、费用
2.网络优化问题关键
点和连线的抽象
延申
1.网络中心
其余点到该中心点距离和最小
2.网络重心
加权系数的中心法
网络计划(一)
问题:是集中精力办大事,还是事事上心求周全?
工程网络图绘制方法
1.准备工作
将整个工程分解为若干工序
确定各工序的前后顺序(紧前、紧后)
确定工序完成时间
t=\frac{a+4m+b}{6}
三点估计法:最乐观时间a、最可能时间m、最悲观时间b
2.绘图顺序
按工序先后从左至右
3.图的结构
节点(事项)
:相邻工序的时间分界点,用
i
表示。
弧(箭线)
:
i
—>
j
表示工序;
i
j
为工序的起点、终点。
相邻弧
:工序前后衔接关系,称紧前(后)工序。
权
:工序的完成时间。
4.绘图要求
注意:图中
不得有缺口、回路和多重边
缺口:多个始点或多个终点的现象(应当只有一个始点和终点)
回路:方向一致的闭合链
处理方法:
查找错误,重新画图
多重边:两点间有多于一条的边
处理方法:
增加虚工序
注意
1.不急于画出工序结束节点
2.节点编号采用“箭杆删除法”
引入虚工序
1.两个工序A、B有相同的始点和终点
2.同时有多个起点(终点)
关键路径法
工程完工期
:终点的最早开始时间
事项开始时间
t_g(1)=0
t_g(j)
=max{
t_E(i)+t(i,j)
}
j=2,3,...,n
关键工序:工序机动时间=零
关键路径:
R(i,j)=0
的关键工序 工序总时差:工序最晚开始时间一工序最早开始时间
事项最晚开始时间:
t_L(n)=t_g(n)
t_L(i)
=min{
t_L(j)-t(i,j)
}
(i=n-1,n-2,...,1)
总结
完工期=终点最早开始时间
关键工序=总时差为零的工序
网络计划(二)
问题:是集中精力办大事,还是事事上心求周全?
计划评审技术PERT
1.PERT与CPM的区别
CPM工序时间确定
PERT工序时间及完工期随机
T \sim N(T_E,\sigma^2)
网络计划的优化
绘制工程网络图—>确定关键线路—>初始计划方案—>网络计划优化
考虑进度(工期优化)+合理利用资源(时间资源优化)+降低费用(时间费用优化)=优化目标
工期优化
压缩关键工序时间
,eg.改进技术、改进工艺、改进设备、保证人/物力
非关键工序时差
,eg.合理调度、抽调人/物力、支援关键工序
采用交叉作业和平行作业
,eg.相连几道工序交叉进行,将一道工序拆成几道平行进行 如果出现两条关键路径,如何压缩工期?
在两条关键路径上压缩同样的时间
时间一资源优化
步骤
1.计算工程每单位时间内所需资源量
2.作出初始资源需求曲线
3.进行资源均衡调整求得新的进度计划
4.评价工程进度计划对资源利用的均衡程度(通过方差评价)
方法
优先安排关键工序所需要的资源
利用非关键工序总时差,错开工序开始时间,错开资源负荷高峰
根据计划规定适当延长项目的工期
时间费用优化
工程成本费用=直接费用+间接费用
优化步骤
1.计算工序费用增加率
2.在网络计划图找出
费用增加率最低
的一项关键工序或一组关键工序作为缩短持续时间的对象
注意:关键工序缩短后的值不能小于最短持续时间,不能成为非关键工序
3.计算相应的增加的总费用
4.考虑由于工期的缩短间接费用的变化,计算项目的总费用
5.重复以上步骤,直到获得满意的方客止
总结
计划评审技术
给定时间的求完工概率
给定概率的求完工期
网络计划优化
时间优化:注意关键路线变化
资源优化:搞平均主义
费用优化:关注直接费用率
排队论
问题:是有求必应坦荡荡,还是随机应变皆欢喜?
排队系统的组成
输入过程+排队规则+服务机构
输入过程 :顾客来源/顾客到达排队系统规律
1顾客的数量
有限m?无限
\infty
?
2顾客到达的方式单个到达?成批到达?
3顾客相继到达的间隔时间分布确定?随机?分布参数?独立?平稳?
排队规则:|顾客排队等待队列和接受服务次序
即时制、等待制、混合制
队列 顾客中途退出?多列间相互转移?
次序 先/后到先服务随机/有优先权
系统容量有限制
等待时间有限制
服务机构:服务台机构形式和工作情况
1数目和排列
单台?多台?并列?
2服务方式
单个/成批服务?
3服务时间
确定?随机?分布参数?独立?平稳?
排队模型的表示
排队模型(X/Y/Z/A/B/C)
X:顾客到达时间间隔的分布
Y:服务时间的分布
Z:服务台个数
A:系统容量
B:顾客源数量
C:服务规则(可省略)
eg.
(M/M/1/\infty/\infty/FCFS)
到达时间间隔为负指数分布
服务时间为负指数分布
1个服务台
系统容量无限
顾客源无限
先到先服务
排队系统的指标
系统的状态n 系统中的顾客数
系统的瞬态
P_n(t)
考虑在时刻系统的状态为n的概率(难求难用)
系统的稳态
P_n
,系统的瞬态的极限
lim_{n \to +\infty}P_n(t)
(
统计平衡状态的解
)
人数指标
队长:
系统中的顾客数n状态概率
p_n
均值
L_s
排队长:
系统中正在排队等待的顾客数均值
L_q
队长=排队长+正被服务的顾客数
时间指标
逗留时间
一个顾客在系统中停留时间W均值
w_s
等待时间
一个顾客在系统中排队等待时间均值
w_q
逗留时间=等待时间+服务时间
其他指标
忙期
服务机构连续繁忙的时间长度
损失率
由于顾客被拒绝使企业受到损失
服务强度
服务机构的繁忙程度
解的应用
研究排队系统运行效率
估计服务质量
确定系统参数 最优值
评测排队系统结构是否合理
研究设计排队系统
总结
1.排队系统组成
输入过程+排队规则+服务机构
2.排队系统指标
人数、时间、强度
3.排队心理学
从排队指标着手设计
博弈论
问题:是只要我想,还是换位思考?
博弈的基本概念
博弈现象:竞争的各方总是想用最好的策略击败对方,取得尽可能好的结果
博弈组成
局中人按规则考虑其他局中人采取策略集在策略集选取策略得到回报采取策略
博弈三要素
局中人+策略+赢得函数=博弈
局中人
参与竞争的各方:人、集团
有决策权的主体,不是参谋或从属人员
二人博弈:两个局中人
多人博弈:多个局中人是否结盟?
策略
局中人所拥有的对付其他局中人的方案集合
在静态博弈中,策略是一个
独立的完整的
行动
不能是若干相关行动中的某一步
局势:每个局中人的策略选择形成的策略组
赢得函数
一局博弈后各局中人的输赢得失
赢得函数的取值与局中人选定的策略有关
“得失”是“局势”的函数
博弈论的研究假设
局中人是理性人
理性人有一个很好
定义的偏好
面临给定约束条件下
最大化
自己的偏好
理性的决策:
换位思考
,预测其他局中人的反应
博弈的分类
局中人对信息掌握情况
完全信息博弈
不完全信息博弈
局中人采取行动的次序
静态博弈
·局中人同时采取行动
·互相保密情况下采取行动
动态博弈
·局中人采取行动有先后
·后采取行动的人可观察到前人采取的行动
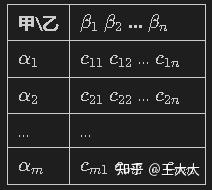
博弈三个要素的矩阵表示
局中人 甲、乙 策略
S_1
={
\alpha_1,\alpha_2,...,\alpha_m
},
S_2
={
\beta_1,\beta_2,...,\beta_n
}
赢得函数
a_{ij}=F(\alpha_i,\beta_j)
二人零和博弈
G={
S_1,S_2;A
}
甲乙决策依据:从
最不利
的情形中,选择
最有利
的情时
甲决策取得收益
最大最小原则
max_i min_j a_{ij}
乙决策避免损失
最小最大原则
min_j max_i a_{ij}
如果 max_i min_j a_{ij} = min_j max_i a_{ij} = a_{i^*j^*}
最优策略 (\alpha_{i^*},\beta_{j^*})
博弈值 V_G=a_{i^*j^*}
二人非零和博弈
问题:是精致利己,还是胸怀天下?
纳什均衡
其他局中人
不改变
策略
任何一方
单独改变
策略
只能带来
收益减少
在二人零和博弈中,双方最优解是一种
均衡解
每个局中人的策略对其他局中人策略的
最优反应
在任何非合作有限博弈中
至少存在一个
纳什均衡

非合作有限博弈存在至少一个纳什均衡
纳什均衡是每个局中人的策略对其他局中人策略的
最优反应
多重纳什均衡与聚点
联系决策背景选取聚点
总结
1博弈基本概念
模型三要素、基本假设、分类
2二人零和博弈
局中人决策原则:换位思考、最大化偏好
3二人零和博弃最优纯策略
收益矩阵存在鞍点
4.纳什均衡
对其他局中人策略的最优反应,非合作有限博弈中存在
5.二人非零和博弈
个人最优v.s.全局最优?
6.多重纳什均衡
联系决策背景确定聚点
延申
1.策略的优超性 化简矩阵,减少计算量
2.二人零和博弈混合策略
多次博弈、交替使用策略/对策略有偏好
局中人决策为线性规划问题(对偶)
3.二人非零和博弈混合策略
通过建立线性规划模型求解最优混合策略
通过期望收益相等关系求解收益矩阵为二阶的问题
使用专业的线性规划软件Lingo
官方网站
https://www.
lindo.com/
LINGO 可以用来求解线性,非线性和整数规划问题。
LINGO NL (LINGO2) 可以用来求解线性,非线性和整数规划问题。
