解理解范畴中的高阶结构和弱等价之间的对应,会使得我们对数学的理解更上一个台阶。
撰文 | 叶凌远
前言
今天这篇文章是
集合论 vs 范畴论 = 汇编语言 vs C++?|范畴论哲学 I
的续篇。上一篇文章中,我们的目光主要集中在范畴内部,讨论范畴论作为一套数学语言,它如何从物体的关系(使用、功能)的角度从而更加准确地对描述了我们日常对数学
结构
的理解。换句话说,使用范畴论的语言,我们自然而然地会在
同构
的意义下理解数学。但同构只是数学研究中等价关系中的一种;对于不同的等价关系,我们需要有一种更为广泛的语言来叙述其性质,这就是范畴论的一个推广——高阶范畴的语言——所提供的。这篇文章从一个更为广泛的等价的概念出发,粗略地介绍高阶范畴的哲学思想和我们理解数学中不同的等价所具有的关联。全文共5000 字左右。
等价与不变性
什么时候两个数学物体是等价的?研究不同数学分支的人会对这个问题有不同的答案。
研究经典代数的可能会说:两个代数结构是等价的,当且仅当它们是同构的;
研究点集拓扑的可能会说:两个拓扑空间是等价的,当且仅当它们是同胚的;
研究同伦论的可能会说:两个拓扑空间是等价的,当且仅当它们是(弱)同伦等价的;
研究数理逻辑的人可能会说:两个逻辑系统是等价的,当且仅当它们具有相同的模型(参考
范畴逻辑 I——逻辑与数学结构的对应
);
研究证明论的可能会说:两个逻辑系统是等价的,当且仅当它们之间可以相互翻译且具有相同的证明论性质。
可以看出,对于不同的数学对象,我们有不同的自然的等价概念;更为重要的是,即使是对于相同的数学对象,在不同的语境中,我们也有不同的等价概念适用与它们(例如上面提到的拓扑空间、逻辑系统等等)。在这种情况下,往往一种等价的概念要弱于另一种,如拓扑空间(弱)同伦等价的概念弱于同胚,逻辑系统具有相同的模型弱于它们之间可以相互翻译。
为什么有这么多等价的概念,甚至对于相同的对象有不同的等价性概念?这与我们想考虑的不同的数学构造、性质的
不变性 [invariance]
息息相关。换句话说,对于每一类“自然”的数学构造和性质,都有一个对应的
等价概念
,其意义在于在这个等价概念下,数学对象关于这一类构造和性质具有
不变性
。例如,我们为什么希望考虑拓扑空间之间的同伦等价?因为现代数学研究拓扑空间最为重要的数学工具是,在代数拓扑中定义的各种代数不变量,而我们对拓扑空间构造的所有代数不变量关于同伦等价都是不变的。换句话说,对于拓扑空间的代数不变量这一性质,其自然对应的等价的概念应该是同伦等价,而不是同胚。
在前一篇文章
集合论 vs 范畴论 = 汇编语言 vs C++?|范畴论哲学 I
我们提到了,范畴论的语言在很大意义上便是为了处理在同构意义下不变的数学——在大部分数学分支中,几乎我们遇到的所有重要数学对象的性质都是关于同构不变的,这也是为什么范畴论如此重要的原因。
我们还是把范畴论的语言与更经典的集合论的语言做一个对比,在集合论中,所有的数学最开始都是非常“严苛”的:每一个集合都由它其中的元素完全决定,拥有不同元素的集合——即使它们是同构的——在集合论的语言下它们也是不相等的;而在集合论的语境下,我们对于同构对象具有相同的数学性质这一点的把握,要么直接储存在我们的脑海中,要么在更为复杂的情况下,成为一个数学定理明确地出现在教材或论文中。但范畴论的语言则不是如此:从最开始,在范畴论的框架下定义的所有概念、证明的所有定理,都是
关于同构不变的
。换句话说,范畴论的语言从最开始就处理好了数学概念以及数学定理跟同构之间的不变性,不需要我们再花费更多的力气。如果你采用了范畴论的语言,那么自然而然地,你做的一切工作都应该对同构是不变的,这就是改换一套数学语言所能够带来的巨大威力。
尽管范畴论已经渗透到了现代数学中的各个分支,但在本科的数学教学或某些更加古老的数学研究分支中,还是很少采用范畴论的语言。其中一个很大的原因是,在这些领域内,其关心的问题中所涉及到有关同构的不变性都很简单,或者很显然,因此在这种情况下,是否采用范畴论的语言变得不那么紧迫。但随着现代数学的发展,当我们考虑的数学不变量更加复杂,采用范畴论的语言就显得更为重要。最为关键的是,现代数学不仅仅关心同构不变意义下的不变量了。对于许多的数学构造,如之前提到的拓扑空间的代数不变量,是对于一些更弱的等价概念不变的。例如在同伦论的语境下,数学家希望得到的是一种“同伦不变” [homotopy coherent] 的数学叙述方式。此时数学家发现,继续采用集合论的语言甚至变得根本不可能了,因为这种等价性的叙述涉及到了许多范畴的高阶性质——我们将在下一节更加详细地阐述这一点。数学在这个方向的进展,使得许多原本曾经认为范畴语言是“abstract nonsense”的数学家现在也开始不得不采用(高阶)范畴的语言。
弱等价与高阶范畴
之前我们提到了,随着数学的发展,许多我们关心的数学对象的性质并不只是在同构的意义下是不变的,而是对于一类更弱的等价性不变,这使得我们会研究这一类弱等价的性质。在这一节中,我们会更加详细地谈谈弱等价与高阶范畴之间的联系。
我们以范畴之间的等价性为例。对于知晓一定范畴论的读者想必都会知道,对于两个范畴 和 ,同构并不是它们间最自然的等价概念,而应该考虑的是范畴等价 [categorical equivalence] 的概念。按照我们之前的观点,等价的概念总是与一个范畴紧密联系的。我们便来详细地探讨一下所有范畴之间构成了一个怎样的范畴。
此处稍微离题一些。对于那些对数学基础 [foundation of mathematics] 较为敏感的读者而言,“所有范畴构成的范畴”这个短语可能是不严谨的,因为这样不加限制的全称量词可能会导致和罗素悖论相似的问题。在范畴论的文献中,解决这个问题的办法一般是引入一个“小”和“大”的相对概念。例如,我们说一个范畴 是“小”的,当且仅当 的物体和态射构成一个集合;若它们不是一个集合而是一个类 [class],则我们称其为一个“大”的范畴。当然,这个分类还可以继续,有“小”“大”“更大”等等。当我们说所有范畴构成的范畴时,可以理解为我们指称的对象是那个所有“小”的范畴构成的“大”范畴。由于一般使用范畴论语言的人都不太关心数学基础的问题,在之后的讨论中我们并不会如此严格地区分“小”和“大”的概念。
要考虑所有范畴构成的范畴,自然而然地我们需要考虑什么是范畴之间的态射。由于它们非常重要,数学家给了它们单独的名字,称为
函子 [functor]
。显然,一个类型为 的函子必定需要将 中的物体映射到 中的物体,将 中物体间的态射映射到对应 中物体间的态射,且需要满足一定的性质。
我很喜欢对函子如下的一个比喻:如果我们把一个范畴当成某一个世界或某一种景观,一个函子就像是一个相机,提供了一个世界到另一个世界、或一个景观到另一个景观的一个照相。有很多简单的例子,例如,我们可以将集合的范畴 嵌入拓扑空间的范畴 中,即有了一个 的照相;我们只需要将所有的集合赋予其上的离散拓扑,则集合间任意的函数在离散拓扑下都是连续的。这个照相具体实现了我们脑中,将集合理解成离散的点构成的空间的直观。一个更加不平凡的例子是,有一个从几何世界 (这个是带基点的拓扑空间构成的范畴,即其物体是拓扑空间加上其中的一个点,态射是保持基点的连续映射)到代数世界 的照相,
这个函子将每个带基点的拓扑空间 映射到其以 为基点的基本群 [foundamental group] ,这便是之前提到很多次的拓扑空间的一个代数不变量。
在函子作为态射下,所有的范畴构成了一个(大的)范畴 。因此很自然的,我们有范畴之间同构的概念:和其他范畴内的同构一样,两个范畴 之间是同构的,当且仅当存在两个函子 ,,使得它们复合后两边都是恒等函子:
但同构并不是最自然的范畴之间的等价概念。内在原因是, 这个范畴相较于其他的范畴而言,它具有
高阶态射
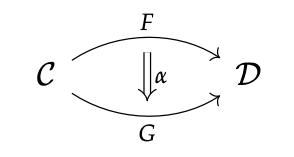
的概念。即不仅两个物体(范畴)之间有态射(函子),态射之间还存在一个态射到另一个态射的态射。用语言表述有些绕,但这个观点可以很直观地用如下的图像描述:
我们把如 这样函子之间的态射称为函子间的
自然变换 [natural transformation]
。按照一贯的风格,我们不会给出自然变换精确的数学定义。但我们同样可以按照之前将函子理解为照相机的比喻,对自然变换有个初步地把握:假如我们有两个相机 分别把世界 映成了世界 中的两个不同的相片,那么从 到 的一个自然变换便像是这两张相片之间的一个连续的转换——正如在一个电影或动画中从一个画面连续地转换到另一个画面。
在函子之间存在的自然变换表明,所有范畴构成的这个大的范畴 比一般的范畴多出了一些高阶的结构,即还存在态射之间的态射。对于这样一类的结构,即有物体、态射和态射之间的态射的一个集体,我们称之为一个
2阶范畴 [2-category]
。 就是一个典型的2阶范畴。对应地,一般的范畴也可以叫1阶范畴 [1-category]。
对于任意一个2阶范畴 ,其内都有一个自然的比同构更弱的等价概念。对于任意 中的两个物体 ,我们说这两个物体在 中是
等价 [equivalent]的,当存在两个态射 , 满足一定的条件;但我们并不要求 这两个复合都等于
恒等态射——满足这样性质的物体是同构的,这也是一般一阶范畴中的等价概念——而是要求这两个复合和恒等映射之间存在着一个“
2阶的同构
”,即存在态射之间的变换使得如下成立:
特别的,如果 是同构的,则它们也是等价的(上面的2阶同构可以取成一个态射到自身的恒等2阶变换),即在2阶范畴中,等价是比同构更弱的一个概念。如果大家熟悉范畴之间的等价概念,则会知道,两个范畴是等价的当且仅当它们在 这个2阶范畴内是等价的。
为什么我们要考虑2阶范畴中这种更弱的等价关系呢?这是因为,在2阶范畴的语境下,
所有自然的数学构造都关于等价是不变的
,而不只是同构。正如在1阶范畴的语境下,所有泛性质 [universal property] 构造都是在同构的意义下定义的,在2阶范畴的语境下,所有对应的(2阶)泛性质构造都是在这种更弱的等价的意义下定义的;换句话说,在2阶范畴中等价的物体对于我们关心的性质而言是没有区别的。以范畴为例,等价的范畴几乎会保持所有我们关心的性质,如极限和余极限的完备性等等。因此,在这个语境下,这种更弱的等价才是我们应该考虑的自然的等价定义。
上面的讨论说明,范畴中的高阶结构会自然对应着某种更弱,但在高阶范畴的语境下更自然的等价定义:我们不再要求两个态射复合后为恒等映射,而是要求复合后的映射和恒等映射之间存在着某种高阶的同构。这个一般的陈述不仅仅适用于2阶范畴,它更广泛地适用于所有n阶范畴 [n-category]、甚至是无穷范畴 [∞-category]。甚至在高阶范畴中,一切概念都应该在这种“高阶同构”的意义下来理解。例如,态射的复合将不是严格定义的,而是在相融的高阶同构 [coherent higher isomorphism] 的含义下定义的。这样的高阶结构,对于现代许多以同伦论为基础的数学来说是非常重要的。
上面这一段话可能有些抽象,如果没有完全理解,没有关系。这篇文章希望大家主要理解的是如下的哲学观点:在数学中,我们希望我们所使用的数学语言能够
自动地处理所有我们关心的(弱)等价的概念及等价物体之间数学性质的不变性
,这一点可能是采用(高阶)范畴论语言研究数学最重要的益处;且以现代数学的复杂程度来说,采取这样的语言已经不再是个人审美的选择,而成为了一种必要。但我们也可以反过来看这一点:一旦当你研究的数学对象有一个比同构更弱的自然的等价概念,这些数学对象之间就非常自然地就构成了某种高阶的范畴模型。甚至有些数学家会说,对于高阶范畴而言,最重要的便是其中弱等价的概念。
结语
在这篇文章中,我们从(弱)等价与不变性的角度阐明了(高阶)范畴论的意义,以及采取这样的语言所能够带来的好处。事实上,高阶范畴之所以越来越重要,某种程度上是因为数学家、逻辑学家、计算机科学家和更多专业人士开始意识到,对于他们所关心的数学对象之间都有一个非常自然弱等价的概念!拓扑空间有同伦等价性,逻辑系统间有弱表示等价性,计算结构之间有弱模拟等价性,等等。这些都使得高阶范畴论的语言在现代研究中占据着越来越重要的地位。理解范畴中的高阶结构和弱等价之间的对应,会使得我们对数学的理解更上一个台阶。
 京公网安备 11010502034662号
京公网安备 11010502034662号