传热学之黑体辐射定律

前言：图解普朗克黑体辐射定律，维恩位移定律，斯蒂芬玻尔兹曼定律。

普朗克黑体辐射定律 描述，在任意 温度 T下，从一个 黑体 中发射出的 电磁辐射 的 辐射率 与 频率 彼此之间的关系。

一定温度的黑体在特定波长的辐射出射度（单位面积的辐射功率），也叫光谱辐射出射度，可用如下公式表示。

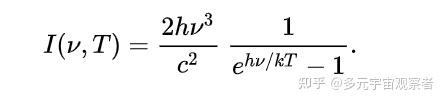
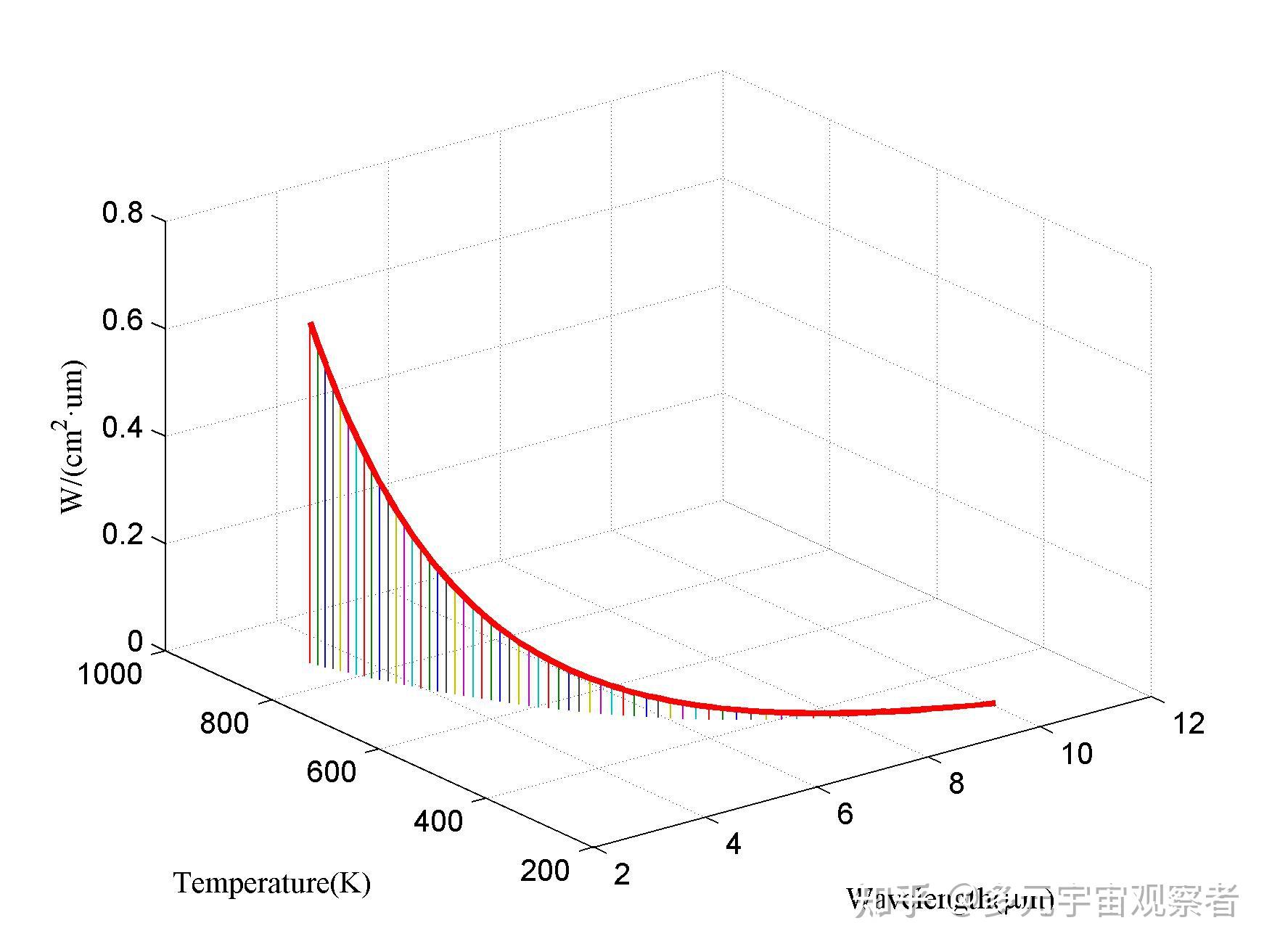
可见，辐射出射度是温度和频率（波长的函数）。使用matlab对不同温度黑体在不同波段的辐射出射度进行计算，可以得到如下图所示的3D图形。

其中红色曲线为维恩位移定律曲线，描述了黑体辐射峰值与温度的关系。可见，随着温度的升高，辐射峰值向短波方向移动。

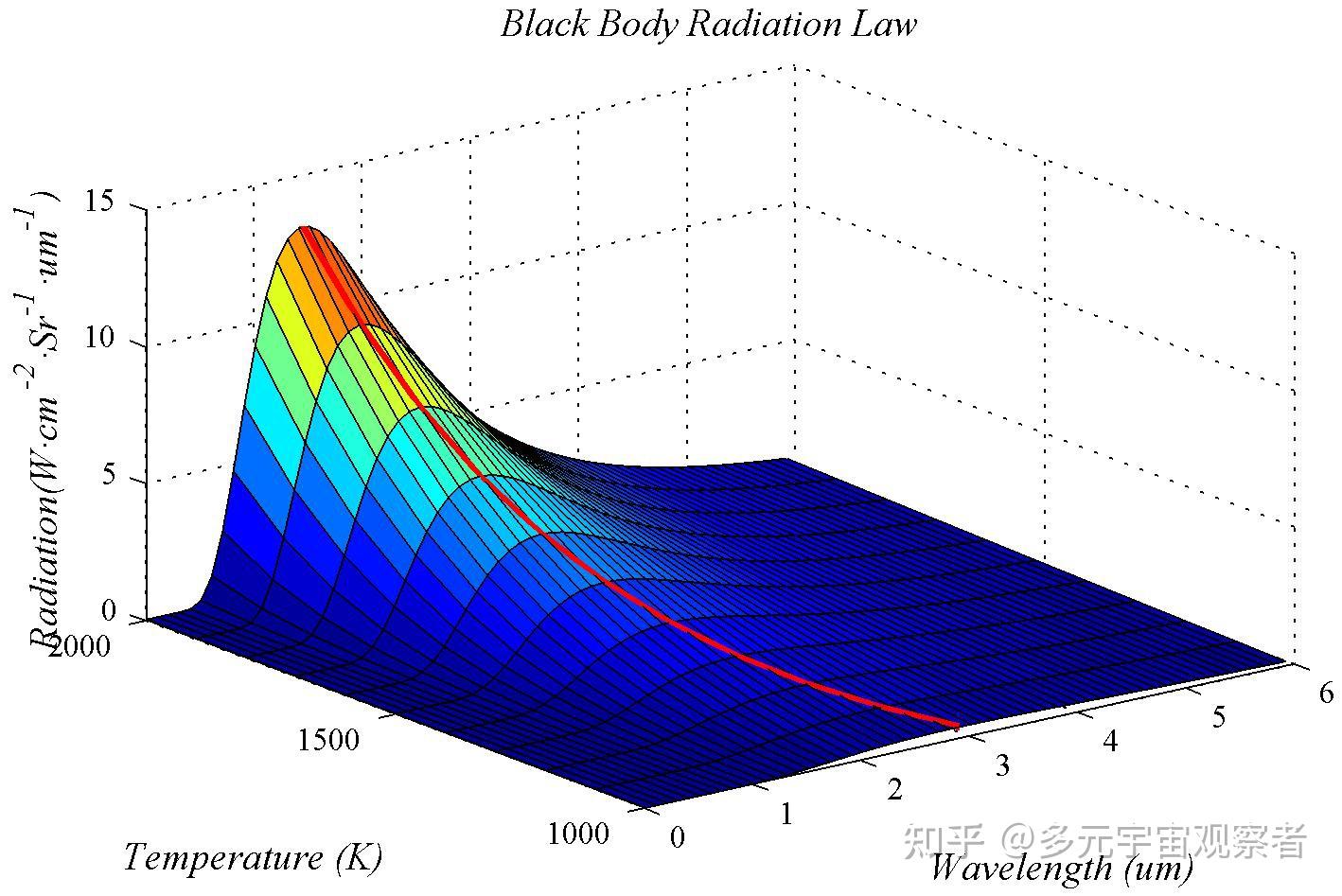
通常，教科书上呈现的是图2所示的图形。但明显图1所示的图形更加直观。

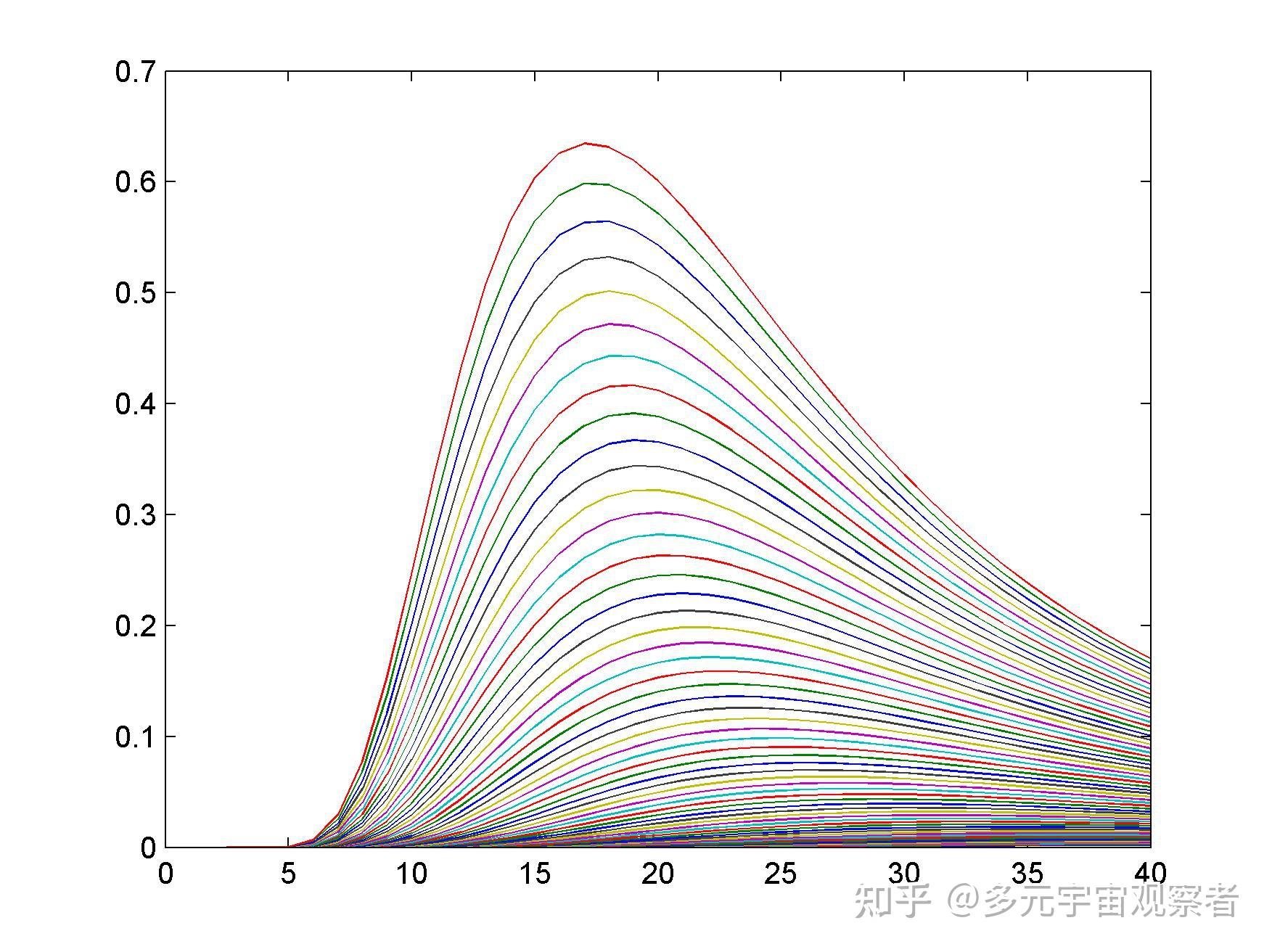
温恩位移定律描述了黑体的辐射峰值与温度的关系。公式如下：

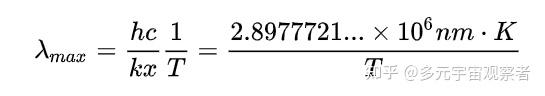
将公式1对所有频率（波长）进行积分，得到黑体的辐射出射度和温度的关系，此即斯蒂芬玻尔兹曼定律。表达式如下：

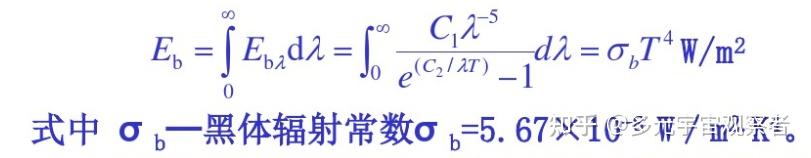
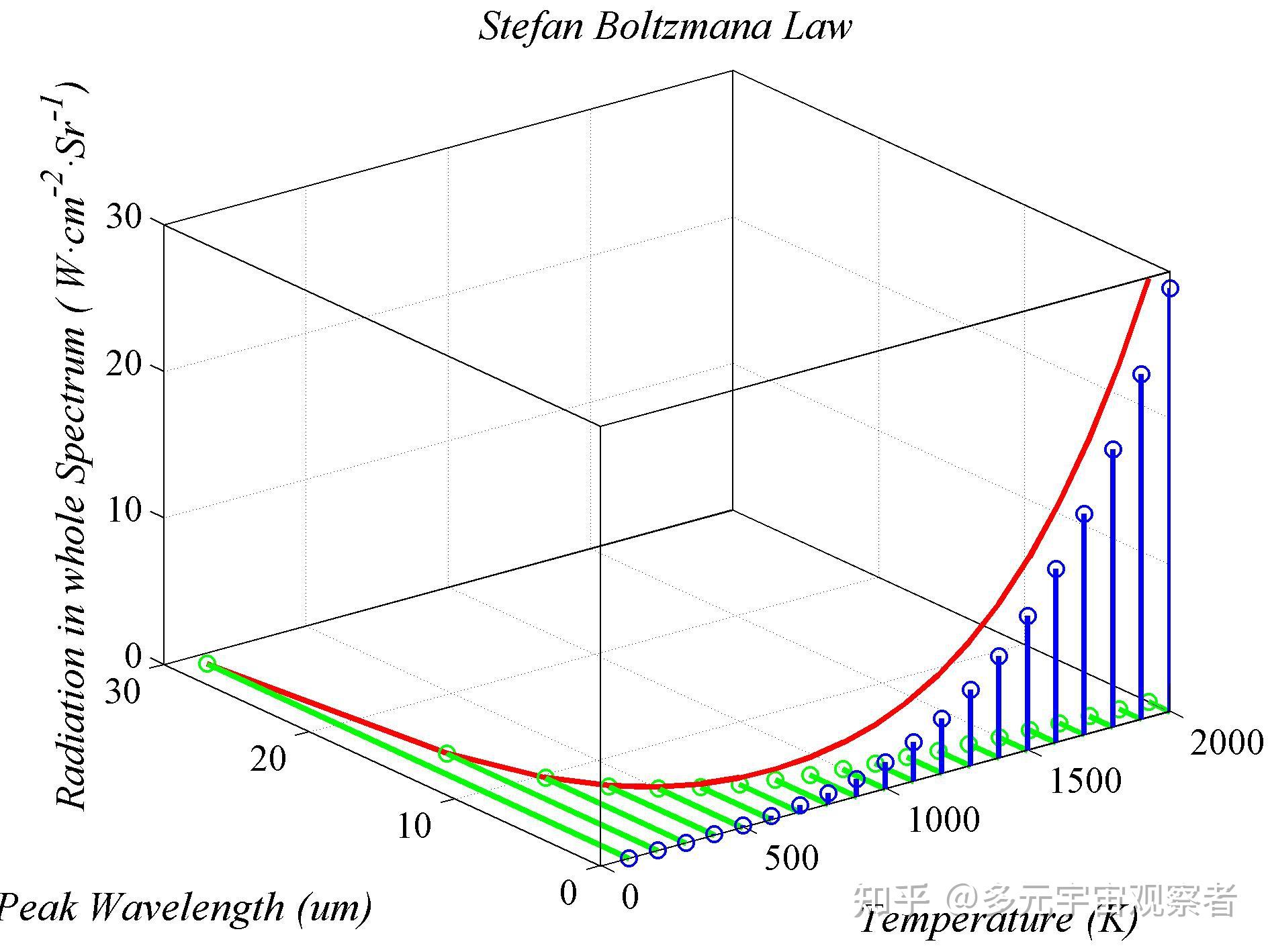
图4描述了不同温度下的峰值辐射波长（绿色线条）和不同温度下的全光谱辐射出射度（蓝色线条）。

公式1除以 2\pi 即可得到光谱辐射亮度（单位面积黑体在特定波长处向单位立体角内辐射的功率），单位 W\cdot m^{-2}\cdot sr^{-1}\cdot\mu m^{-1} 。

一般情况下，我们重点关注黑体（灰体）在特定波段的辐射特性，因此将公式1对特性波段积分，就得到了不同温度黑体在特定波段的辐射出射度。公式如下：

E_{a-b \mu m}(T)=\int_{a\mu m}^{b \mu m}E(\lambda,T)d\lambda

例如，研究红外辐射在大气中传输时。重点关注三个波段，1~3μm，3~5μm，8~14μm，亦俗称的大气窗口。

则不同黑体在以上三个波段的辐射出射度如下

E_{1-3 \mu m}(T)=\int_{1\mu m}^{3 \mu m}E(\lambda,T)d\lambda

E_{3-5 \mu m}(T)=\int_{3\mu m}^{5 \mu m}E(\lambda,T)d\lambda

E_{8-14 \mu m}(T)=\int_{8\mu m}^{14 \mu m}E(\lambda,T)d\lambda

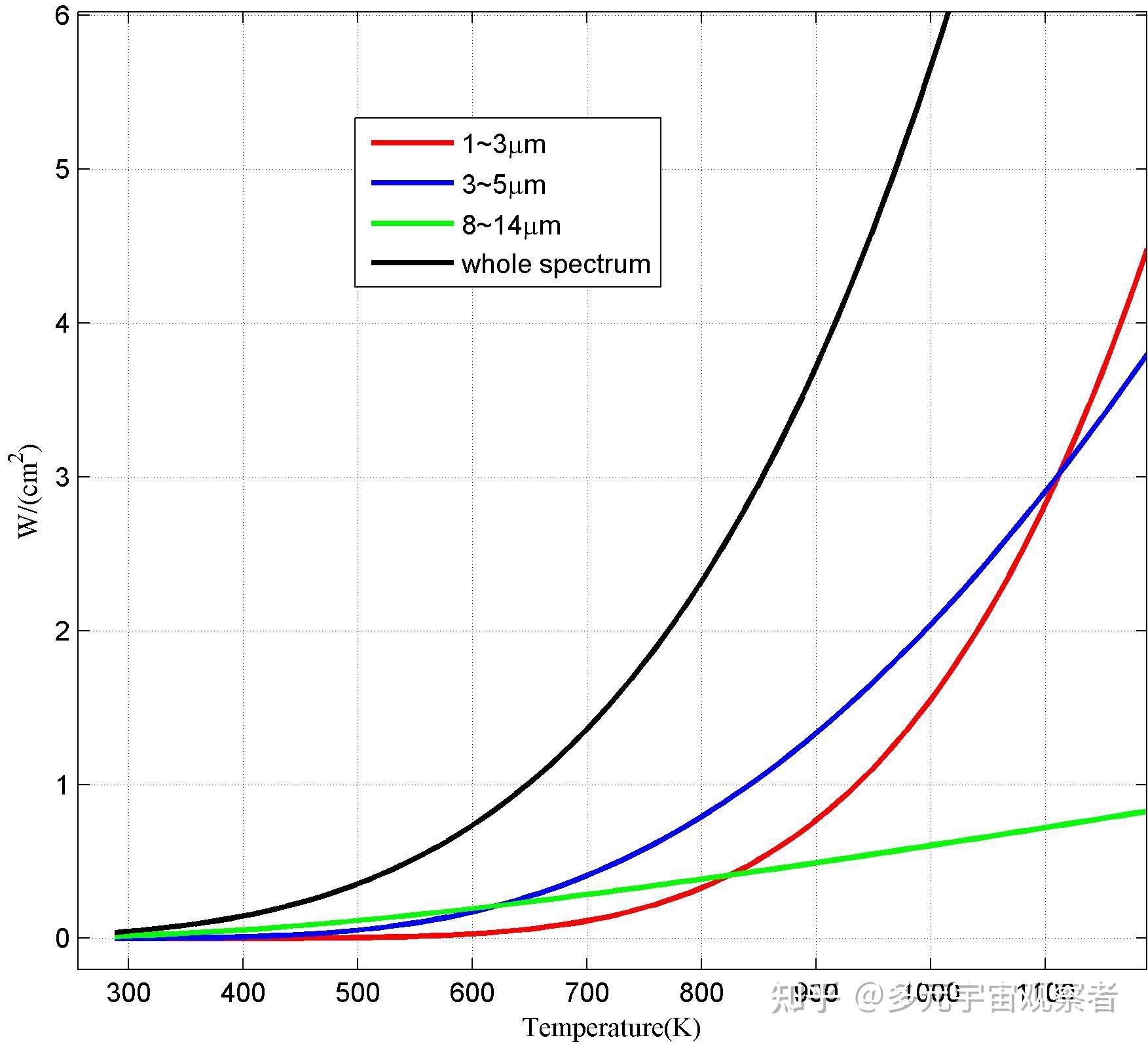
由图5可知，不同温度黑体（灰体）在不同波段的辐射特性不同。

温度在600K（326.85℃）以下时，黑体（灰体）辐射以长波辐射为主，长波>中波>短波。地面装甲车辆的辐射特性基本处于该温度范围。

温度处于650K~1100K（376.85℃~826.85℃）之间时，黑体（灰体）辐射以中波辐射为主。尤其当温度在820K以下时，中波>长波>短波；当温度在820K以上时，中波>短波>长波。武装直升机及运输机发动机的辐射特性基本处于该温度范围。对于此种目标，采用中波制导武器最容易锁定目标。

当温度进一步上升，温度大于1100K（826.85℃）时，目标以短波辐射为主。战斗机及导弹尾焰的温度通常高于此温度，因此对于此类目标，采用短波红外制导武器最为有效。

源代码如下（代码原创，转载请注明出处！）：