首发于 DH的学习笔记

切换模式

投资组合理论（一）：Markowitz均值-方差模型

JackyDai

Quant小白

新开一个专栏，用作记录一些学习笔记。

1 引言

最近打算从头开始复习一遍投资组合和资产定价相关理论，于是先从开山鼻祖的Markowitz均值-方差模型开始。

资产配置主要解决的问题是：如何分散投资从而在风险最小化的同时收益最大化。资产配置的主要目的就是在未来某个时点达成某个预期收益目标，并将资产的波动控制在个人可承受范围内。Markowitz均值-方差模型就是用来求解最优资产配置的比例，其也是首次将数理统计方法引入投资组合理论。

2 理论基础

假设市场上有 n 种风险资产，资产的收益率分别为 r_1,r_2,\cdots,r_n ，投资者在各风险资产上的配置比例分别为 \omega_1,\omega_2,\cdots,\omega_n ，则投资组合的收益率为 r_p = \sum\limits_{i=1}^n \omega_i r_i ，其中 \sum\limits_{i=1}^n \omega_i = 1 .

从而，投资组合的期望收益率为

E(r_p) = \sum\limits_{i=1}^n \omega_i E(r_i)\\

方差为

Var(r_p) = \sum\limits_{i=1}^n \omega_i^2 Var(r_i) + \sum\limits_{i\neq j}\omega_i\omega_j Cov(r_i,r_j)\\

投资者资产配置的前提是对未来形成预期，即 r_1,r_2,\cdots,r_n 的概率分布，然后设定自己的预期收益目标，最后确定在各风险资产的投资比例 \omega_1,\omega_2,\cdots,\omega_n ，达成投资目标。

假设投资者的初始资产为 W_0 ，则未来的资产为 W_0(1+r_p) ，若投资者的效用水平仅与资产水平相关，则效用水平 U(r_p) 也是一个随机变量。从最大化期望效用的角度出发，投资者决策过程就由如下公式展示：

\begin{equation*} \begin{split} &\max_{\omega_i}\, E[U(W_0r_p)]\\ &s.t\quad \sum\limits_{i=1}^n \omega_i = 1 \end{split} \end{equation*}\\

上式可简化为

\begin{equation*} \begin{split} &\max_{\omega_i}\,E[U(r_p)]\\ &s.t\quad\sum\limits_{i=1}^n \omega_i = 1 \end{split} \end{equation*}\\

将 E[U(r_p)] 进行Taylor展开，可以发现，若 r_1,r_2,\cdots,r_n 服从正态分布， 则期望效用完全取决于投资组合收益率的均值与方差 。再假设效用函数是凹函数，则投资者的决策问题为：

\begin{equation*} \begin{split} &\min_{\omega_i}\,Var(r_p)\\ &s.t.\quad \left\{\begin{array}{lc} \bar r_p = \sum\limits_{i=1}^n \omega_i E(r_p)\\ \sum\limits_{i=1}^n \omega_i = 1\\ \end{array}\right. \end{split} \end{equation*}\\\tag{1}

其中 \bar r_p 为投资者的预期收益率。公式(1)说明，投资者的决策过程是，在达成预期收益的前提下，实现投资组合的风险最小化。公式(1)可以用Lagrange方法求解，一阶条件为：

\begin{pmatrix} \Sigma & e & \bar r \\ e^{'} & 0 & 0 \\ \bar r^{'} & 0 & 0 \end{pmatrix} \begin{pmatrix} \omega \\ \lambda_1 \\ \lambda_2 \\ \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ \bar r_p \end{pmatrix}\\

其中 \bar r_p 为 n 种资产收益的期望值构成的列向量， \Sigma 为收益率的协方差矩阵， e 为 n\times 1 的单位列向量。最终投资比例最优解的形式为：

\omega^{*} = a + b \bar r_p \\

即最优解与预期收益率为线性关系。而风险 Var(r_p) 是 \omega 的二次函数形式，下图为预期收益率 \bar r_p 与最优解下标准差的关系：

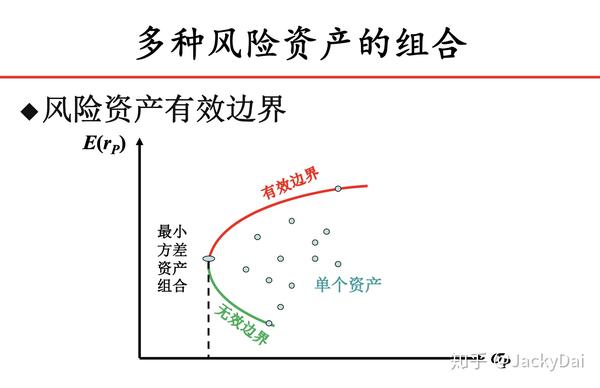
其中上半段曲线被称为有效前沿 (Efficient Frontier)，曲线内的点被称为可行集。

CAL与有效前沿相切时，称该切线为资本市场线 (CML)。

3 实证研究

首先我们从上证指数中选取5只不同行业的成分股，时间为2018-2019年，行业不同是为了让其收益率的相关性尽量低，因为相关性过高的话很难达到风险分散的效果。5只成分股的相关情况如下：

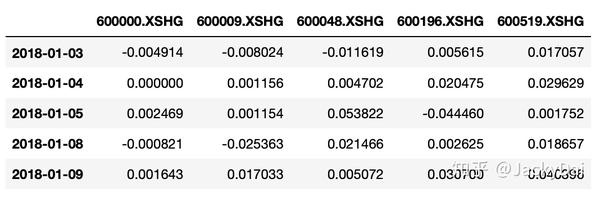
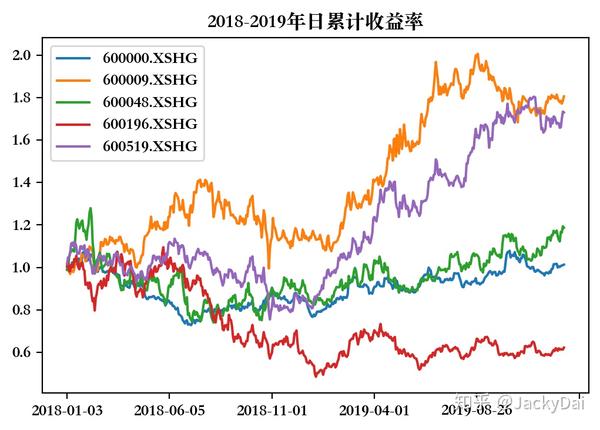
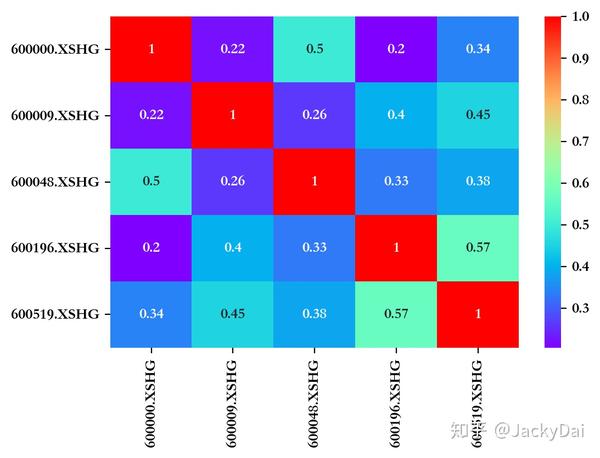
可以看到，5只成分股收益率的相关性较低，满足我们的要求。

接下来，编写一个类以实现Markowitz均值-方差模型的求解：

from scipy import linalg
# 定义类
class Markowitz:
    def __init__(self, returns):
        self.returns = returns
    # 求解最小方差组合
    def solveMinVar(self, goal_ret):
        cov = np.array(self.returns.cov())
        mean = np.array(self.returns.mean())
        row1 = np.append(np.append(cov.swapaxes(0,1),[mean],axis=0),
                        [np.ones(len(mean))], axis=0).swapaxes(0,1)
        row2 = list(np.ones(len(mean)))
        row2.extend([0,0])
        row3 = list(mean)
        row3.extend([0,0])
        A = np.append(row1, np.array([row2,row3]), axis=0)
        b = np.append(np.zeros(len(mean)), [1,goal_ret], axis=0)
        results = linalg.solve(A, b)
        return(np.array([list(self.returns.columns), results[:-2]]))
    # 计算投资组合方差
    def calVar(self, portion):
        return(np.dot(np.dot(portion, self.returns.cov()), portion))
    # 绘制有效前沿
    def plotFrontier(self):