著名的丢番图方程,最有趣的“世界难题”,从古研究至今


2019年9月6日,由布里斯托尔大学和麻省理工学院的研究人员领导的一个团队宣布,他们发现了所谓的“三个立方数和”的问题的最终解,即求方程x³+ y³+ z³= k的整数解,k的值在1到100之间。自1954年提出以来,直到2016年,除了k=33和k=42的两个解之外,所有的解都被找到了。19年3月,数学家安德鲁·R·布克(Andrew R. Booker)发表的一篇论文中宣布,他在布里斯托尔的超级计算机上花费了数周的计算时间,找到了k=33的正确解。
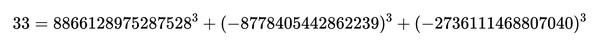
不久后,k=42的解也被发现了(布克和麻省理工学院的安德鲁·萨瑟兰),答案是:
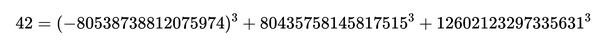
对于k在1到1000之间的值,114、165、390、579、627、633、732、906、921和975的解仍然没有被发现。
丢番图方程
三个立方和的问题是求丢番图方程解的一个例子,它可以定义为:
定义
丢番图方程是一个有几个未知数、系数为整数的代数方程。
也就是说,丢盘方程是有几个未知变量(x,y,z, ……)的方程,它的解(=0)只有当方程的系数是整数时才会出现。
线性丢番图方程
线性丢番图方程是一阶方程,其解被限制为整数。线性丢番图方程为:
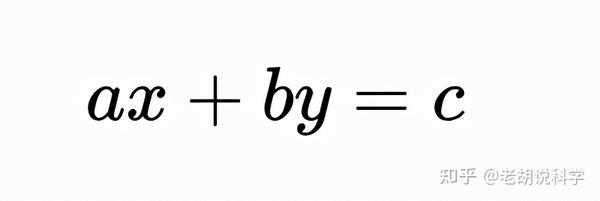
其中a、b、c为整数系数,x,y为变量。例如:
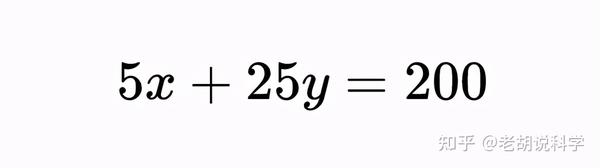
有多少个整数解?因为这是一个有两个未知数的方程,我们不能一次解一个变量(就像一个典型的线性方程组一样)。相反,对于线性情况,我们可以使用以下定理:
线性丢番图方程有整数解当且仅当c是a和b的最大公约数的倍数。
如果整数(x, y)构成给定a,b,c的线性丢番图方程的解,那么其他的解有(x + kv, y - ku)的形式,其中k是任意整数,u和v是a和b的最大公约数的商。
两个或两个以上整数的最大公约数(它们都不为零)是能整除每个整数的最大正整数。对于上面的例子,我们可以先提出公约数5,得到:
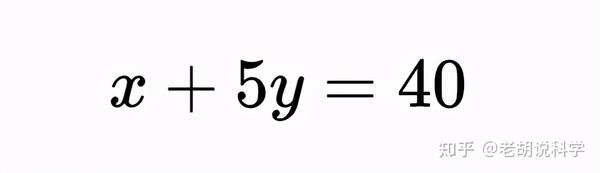
a和b的最大公约数是1和5。任何非负c都是1的倍数。有9个小于或等于40的5的倍数。它们是0,5,10,15,20,25,30,35,40。因此,方程5x+25y=200有9个整数解,他们是:
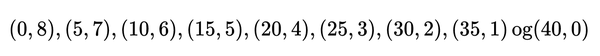
上述过程是丢番图分析的一个简单版本,它是找到丢番图方程的解所必需的过程。在这些分析过程中通常会问到的问题有:
- 有无限或有限的解吗?
- 理论上所有的解都能找到吗?
- 在实践中,人们能计算出完整的解列表吗?
用于求解丢芬图方程的常用方法包括因式分解、不等式、参数化、模算法、归纳法、费马无限递减法、归约为佩尔方程和连分式、位置数字系统和椭圆曲线法。
哈代-拉马努詹方程
哈代-拉马努詹数字——1729,被称为“出租车数”,它被定义为“可以用两种不同方式表示为两个正立方数的和的最小数”。这是英国数学家哈代在医院看望印度数学家斯里尼瓦萨·拉马努詹时发生的一件奇事:
我记得有一次他在帕特尼住院时,我去看他。我坐的是1729号出租汽车,我说这个数字在我看来很沉闷,我希望它不是什么不祥之兆。“不,”拉马努詹回答说,“这是一个非常有趣的数字,它是可以用两种不同的方式表示为两个立方数和的最小数。——哈代(1918)
出租车数的核心方程为丢番图,即:
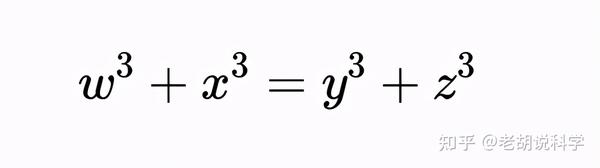
1729可以表示为两个立方数的和(有两个解),它们是1³+ 12³和9³+ 10³。到目前为止,已知的出租车数有6个。它们是:

费马最后(大)定理

- 费马最后定理的原始表述
可以表示为立方数和的数字(如三立方数和问题和哈代-拉马努詹数)最早是在1657年由伯纳德·弗雷尼卡·德·贝西提出的,他在与约翰·沃利斯和皮埃尔·德·费马的书信中引用了1729这个数字来描述这一成果。从那以后,费马的名字在某种程度上就成了这个问题的一般情况的同义词。1637年,费马在丢番图的一本《算术》的空白处断言,三个正整数a、b和c不满足丢番图方程:
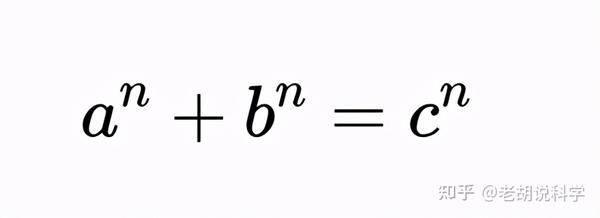
费马在他著名的声明中说他已经证明了n大于2的整数值是正确的(不满足丢番图方程),但他不能把它写在他的笔记中,因为写不下了:
一个立方数不可能是两个立方数的和,一个四次方数不可能是两个四次方数的和,一般来说,任何大于二次方的数都不可能是两个类似的幂的和。我发现了一个非常绝妙的例子来证明这个命题,即这个纸的边距太窄了,写不下。——费马
在经历了358年之后,这个猜想终于在1994年被英国数学家安德鲁·威尔斯在《数学年鉴》上发表的论文“椭圆曲线和费马最后定理”中证明了。怀尔斯的反证法长达129页,用代数几何和数论的技巧证明了椭圆曲线的模块化定理( modularity theorem)的一个特例,它与 里贝特定理 (Ribet’s theorem) 一起证明了费马最后定理的正确性。由于它大量地使用了现代数学,可以肯定的是,威尔斯的证明与费马声称发现的证明方法不一样(费马是否有更高明的证明方法?),费马的方法至今仍未找到。
毕达哥拉斯的三元数组
也许最著名的丢番图方程是费马最后定理中那个方程的一个特例,但对于n=2来说。这个方程可以帮助我们求出直角三角形的边长。
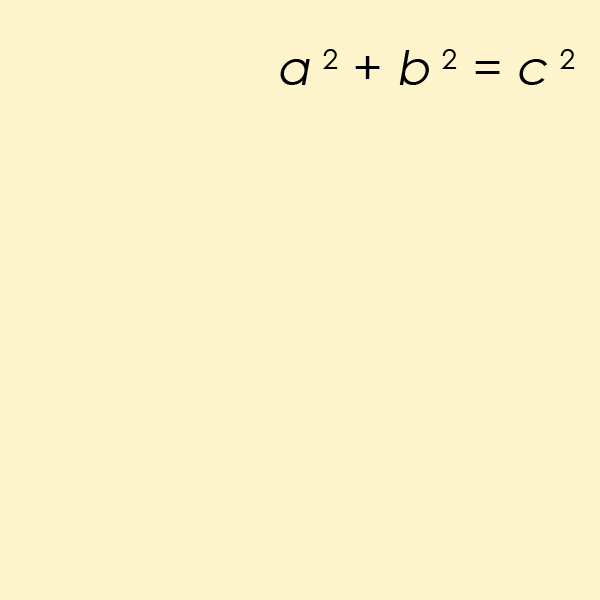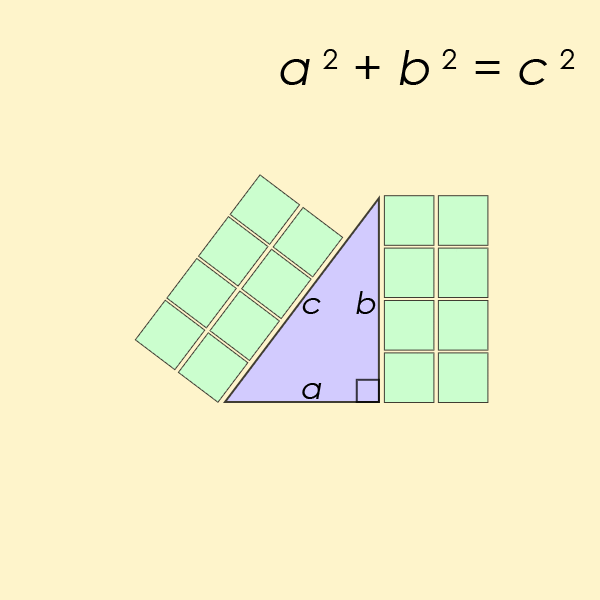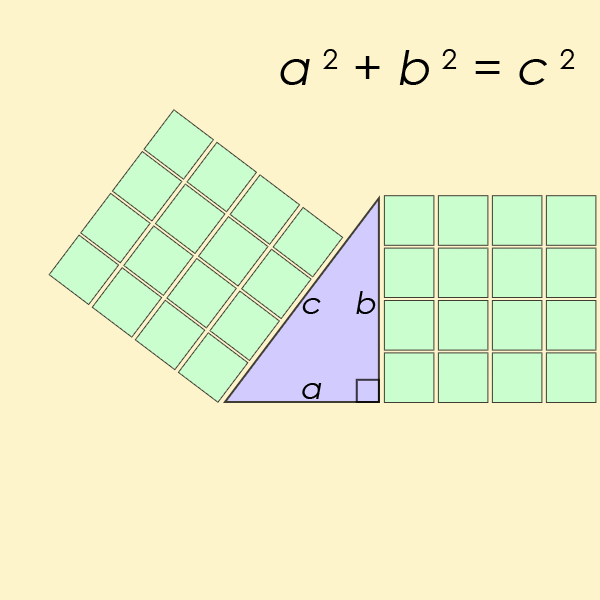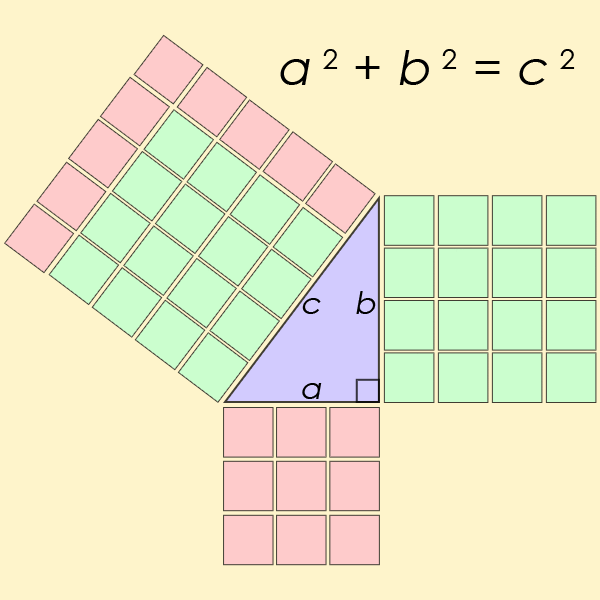
- 动画演示最简单的毕达哥拉斯三元数组,3²+ 4²= 5²
佩尔方程
佩尔方程(有时是佩尔-费马方程)是下列形式的任何方程,其中n是给定的无平方因子正整数,求x和y的整数解:
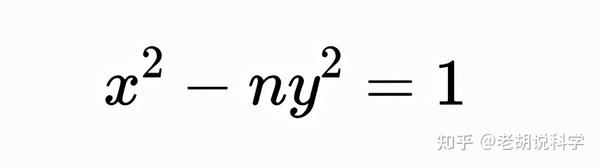
印度数学家Brahmagupta在628年首次广泛研究了丢番图方程。他开发了所谓的“查克拉瓦拉方法( chakravala method)”来解决丢番图方程和其他不确定方程。早在大约一千年前,英国数学家约翰·佩尔(1611-1685)在约翰·海因里希·拉恩(Johann Heinrich Rahn)的指导下研究过它。
早在公元前400年,印度和希腊就研究过佩尔方程(n = 2)这种形式的方程,除了x²−2y²=−1的情况,因为这个方程与计算根号2得到的无理数有联系(如果x和y是满足这个方程的正整数,那么x/y是√2的近似值)。
在笛卡尔坐标系中,方程的形式是双曲线,当曲线经过一个x坐标和y坐标都是整数的点时,方程的解就会出现,例如x = 1,y = 0和x = -1,y = 0。拉格朗日证明了只要n不是完全平方数,佩尔方程就有无穷多个不同的整数解。
欧德斯猜想(欧德斯-施特劳斯猜想)
欧德斯猜想指出,对于每一个大于2的整数,有理数4/n可以表示为三个正单位分数的和。也就是说,对于每一个n≥2的整数,都存在正整数x,y和z,使:
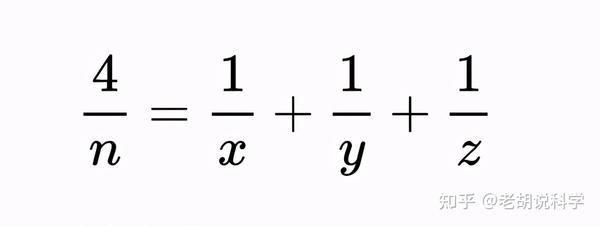
如果n是一个合数(n = pq),那么4/n的展开式可以由4/p或4/q的展开式得到。因此,如果存在反例,构成反例的最小n必须是一个素数。

这个猜想是以数学家保罗·欧德斯(Paul Erdős)和恩斯特·G·施特劳斯(Ernst G. Straus)的名字命名的,他们在1948年提出了这个猜想,至今仍未得到证实。方程的丢番图形式出现在等式两边同时乘以分母,得到其多项式形式:
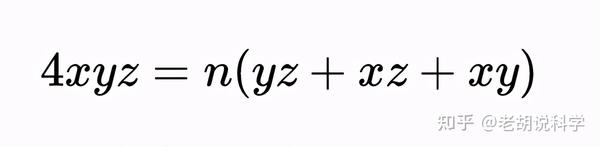
例如,对于n=5,有两种解:
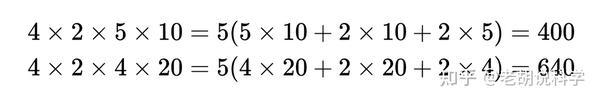
欧拉幂和猜想(欧拉猜想)
伦纳德·欧拉在1769年错误地推测了丢番图方程的形式:
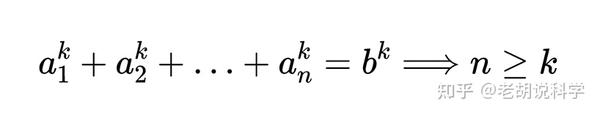
也就是说:
欧拉幂和猜想
对于所有n和k大于1的整数,如果n个正整数的k次方之和是k次方数,那么n大于等于k。
也就是说,如果aᵏ的前n项之和等于其本身的k次幂项(如bᵏ),那么n一定大于或等于k。这个猜想是欧拉为了推广费马最后定理所做的尝试。1966年,兰德和帕金(Lander and Parkin)通过计算机搜索推翻了这个猜想,他们发现了k=5的反例,并在所谓的“有史以来发表的最短论文”中宣布:

- 兰德和帕金。欧拉猜想的反例。
k = 4的特例后来被埃尔基斯(Elkies,1986)否定了,他发现了一种构造无穷级数反例的方法。他举出的最小的反例是:
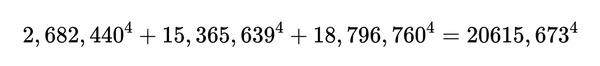
后来Roger Frye(1988)改进了这一点,他利用计算机搜索发现,最小的反例是:
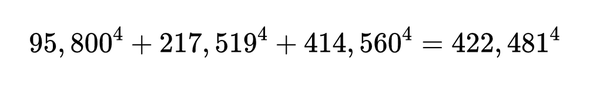
历史
第一个已知的关于丢番图方程的研究是亚历山大的丢番图,他是一位三世纪的数学家,他也把符号主义引入了代数。他是《算术》系列书的作者,其中许多书现在已经失传。
希尔伯特的第十个问题
希尔伯特的第10个问题是,是否存在一种算法来确定任意丢番图方程是否有解。这个问题是大卫·希尔伯特在1900年提出的,是他列出的23个数学开放问题的一部分。希尔伯特的原始表述如下:
希尔伯特的第十个问题:
给定一个含有任意数量的未知量和有理整数系数的丢番图方程,设计一个程序,根据这个程序,用有限的次数就可以确定这个方程是否可以用有理整数解。
这个问题在1970年被尤里·马蒂亚耶塞维奇(Yuri Matiyasevich)解决了,他在他的博士论文中证明了解决所有丢番图方程的一般算法是不存在的。他的解决方案暗示了希尔伯特的第十题的不可解性。

用现代术语来说,希尔伯特的第十题是一个不可判定的问题。也就是说,这是一个决策问题,它被证明是不可能构造一个算法,总是导致一个正确的“yes-or-no”的答案。
想了解更多精彩内容,快来关注老胡说科学