实用的因果推断(一)-基础概念

Lotus

stay hungry,stay foolish

因果推断的核心内容，实际上想办法将未观测到的潜在结果(即反事实结果)估计出来

一.前言

如果说到数据分析的核心技能，抛开基本工具与知识的掌握，业务理解、数据敏感度与分析思维才是关键。其中分析思维，我认为区别于业务数分的关键，是怎么绕开数据的陷阱，得出稳健的结论。

如果只是多维度去拆分，去透视数据，那么业务方也能做，但是他们得出的结论不会稳健。拿工作遇到的推广问题来说，为什么发现某个因素对转化率有益，真正开始提高投放占比的时候，效果却差了很多？又或者，投放中经常会遇到难以分拆出量和质的影响，因为一般而言，购买人数提高了，转化率一般也会下降。这个时候难以判断是策略的影响还是购买量提高带来的。投放不能做出精准的AB实验，因为针对不同账号，不同广告计划，使用不同的投放策略，我们无法去控制购买用户会随机分配到两组，不能实现随机化实验来验证结果。

基于以上，我经常困惑，怎么样的数据分析思维得出的结论才是稳健的，才能正确指导业务方向，才是比业务自己的数据分析更加专业的，而不是说我们的结论，今天适用，明天就不适用了。

我希望从统计，计量经济学，因果推断中，找到科学的分析方法。

二.两种分析悖论

1.辛普森悖论

第一个悖论是我们比较熟悉的辛普森悖论。

美国加州大学伯克利分校研究生录取数据中，男生录取率为44%，女生录取率为35%，那能依据这一观测数据，认为伯克利分校研究生录取存在性别歧视吗？Bicke对此做了研究，他发现，虽然总体上，男士录取率高于女生，但是拆开专业后发现，几乎每个专业均是是女生的录取率更高。

为什么比较总体结论与比较总体各部分的结论会存在差异呢？因为男女生在专业上的分布不一样，男生主要集中在录取率较高的专业，女生主要集中在录取率较低的专业，这样整体来看，就是女生录取率更低了。

		男生			女生
	申请人数	录取数	录取率	申请人数	录取数	录取率
专业1	200	40	20%	400	120	30%
专业2	800	400	50%	100	70	70%
合计	1000	440	44%	500	190	38%

简单的直观印象往往是错误的，需要我们更加深入的分析，才能获取正确的结论。

例如我们在比较两种售卖策略用户的转化率时，如果不同类型的用户在售卖策略间有很强的倾向性，比如购买力强的用户倾向策略A，那么结论可能是策略A转化率优于策略B，但是如果对用户分层，结论可能就相反了。

2.Lord悖论

Lord构造出了一个假想案例。一所大学想考察其食堂膳食对学生体重的影响以及影响的性别差异，收集了在食堂膳食吃饭学生9月入学的体重，又在第二年6月收集了这批学生的体重。

两个统计学家，用不同的分析方法得到了两个相反的结论。

第一个统计学家 ，计算男生和女生入学时的平均体重，分别是130斤和90斤，然后计算第二年6月的男女体重，发现还是130斤和90斤。所以他认为学生食堂膳食对学生体重没有影响。

第二个统计学家 ，采用了更加高级的方法。他控制了个体入学时的体重，选取入学体重相同的男女生的数据，然后构建回归模型，以入学体重作为X，次年体重作为Y，拟合回归曲线，发现同样体重的男生和女生，男生体重增加更大，比女生要高。

现在，我们用因果推断中的 潜在结果框架 来分析这个问题。

因果推断中，Rubin指出，必须要有干预，没有干预就没有因果，这里的干预可以是策略，活动等。对于每个干预，都会有一个潜在结果。一般而言，可以分为干预组和控制组。某些干预的因果效应应该等于干预组和控制组两种状态下潜在结果的差值。

拿Lord悖论的问题来说，研究的是食堂膳食对学生体重的影响。因而，需要两组用户。

干预组 :去学校膳食食堂吃饭的学生

控制组 :不去学校膳食食堂吃饭的学生(可以分为在家吃和外面吃)

第一个统计学家的结论，只有在如果不在学校食堂吃饭，学生次年6月的体重等于其入学的体重，这一假设下才成立。

第二个统计学家的结论，男生平均增长体重超过女生，这一结论是正确的，但是利用这种方法计算的差额也不代表因果效应。类似的，他的结论只有在如果不在学校食堂吃饭，学生次年6月的体重与入学体重成线性关系，这一假设下才成立。

所以，如果要考察在食堂吃饭这一干预的影响，必须比较两种状态下的潜在结果，即有没有在食堂吃饭，分别的体重变化。但是我们只有干预组的数据，拿到的数据只有在食堂吃饭的学生体重。

这也是现实中经常遇到的问题，没有控制组该怎么办？

一些因果推断方法致力于解决这个问题，即预测，构造一个我们无法观测，无法获取数据的控制组。

三.两种分析偏差

1.混杂偏差

考虑以下问题:

变量D表示是否随身带打火机

变量L是否有抽烟的习惯

变量Y表示患肺癌的风险

箭头表示具备因果关系，很明显，如果一个人有抽烟的习惯，他随身带打火机的概率很大。如果一个人有抽烟的习惯，那么他患肺癌的风险也会很大。同时，是否随身带打火机与患肺癌的是没有因果关系的。

但是，如果有人想研究随身带打火机是否对人患肺癌有因果影响，他通过抽样调查获得了D和Y的数据，通过数据发现，随身带打火机的患肺癌的风险更大。D和Y存在 相关性， 这是因为随身带打火机的人，有抽样习惯的可能性较高，从而患肺癌的风险更大。

尽管D和Y没有因果关系，但是因为他们有共同原因L，从而使两者表现出相关性。

D<-L->Y

其中L表示D和Y的混杂因素，混杂因素造成的相关称为混杂偏差。如果我们想要得到D对Y的因果效应，就必须消除混杂因素L的影响。

如何处理混杂偏差？

1.完全随机化实验。随机化实验与控制变量的思想不同，但是作用相同，关键作用是可以平衡两组个体其他因素的分布，使得两组个体的混杂因素(包括可观测与未观测)具备相同的分布。

2.实际工作中，有时无法去做完全随机化实验，很多数据是观测数据。这种情况下，如果能识别出具体的混杂因素，可以利用 回归方法 或 匹配方法 ，以混杂因素为条件，来消除混杂偏差。后续学习中，会接触到具体的分析案例。

2.样本选择偏差

现在我们来看另外一个问题：

变量D表示民族

变量L学习能力

变量Y是否被大学录取

学习能力对能否上大学的影响，不用多说。其中民族因素因为存在优惠政策，存在一定的加分项，所以同样高考成绩，少数民族录取的概率会更大，所以民族因素也会影响到能否上大学。而不同民族的学生，在智力分布上的差距是差不多的，这两者是不存在因果关系的。

但是，如果有研究者去收集大学生的数据，可能会发现民族和学习能力存在负相关性，得出少数民族学生学习能力稍微差一些的结论，这是错误的，存在 样本选择偏差。 因为他只调查了上了大学的同学。

尽管D和Y没有因果关系，但是如果以他们共同影响结果L为条件去获取数据，便会发现相关性，以共同结果为条件造成的分析偏差，称为样本选择偏差。

后续因果分析方法，主要目的是消除这两种偏差，将因果效应识别出来。

四.因果推断基础

4.1 基本概念

干预变量T与潜在结果Y

\begin{array}{l}\text { } T_{i} \text { the treatment intake for unit i. } \\ T_{i}=\left\{\begin{array}{l}1 \text { if unit i received the treatment } \\ 0 \text { otherwise }\end{array}\right.\end{array}

干预变量T代表实验对象有没有接受干预

\begin{array}{l}Y_{0 i} \text { is the potential outcome for unit i without the treatment. } \\ Y_{1 i} \text { is the potential outcome for the same unit i with the treatment. }\end{array}

潜在结果Y代表实验对象在干预或者不干预的条件下的结果

因果推断 的 基本问题 是我们无法观察到经过干预和未经干预的同一实验对象，就好像我们有两条不同的道路，我们只能选一条路前进。

我们将发生的潜在结果称为事实，没有发生的结果称为反事实。

基于以上，我们可以定义个体的干预效果

Y_{1 i}-Y_{0 i}

虽然个体干预效果无法计算，但是我们可以转化计算-平均干预效果ATE(average treatment effect)

A T E=E\left[Y_{1}-Y_{0}\right]

另外一个更容易估计的对象是， 对被干预者 的 平均干预效果。

A T E T=E\left[Y_{1}-Y_{0} \mid T=1\right]

现在，我们会从一个case出发，尝试计算下以上干预效果

假设我们可以观察到所有潜在结果,如下,t表示干预-学生是否使用平板电脑，y表示事实的测试成绩，y0和y1分别表示接受干预和不接受干预下的结果

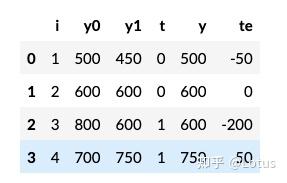
=(−50+0−200+50)/4=−50，这意味着平板电脑会使学生的学习成绩平均降低 50 分

=(−200+50)/2=−75，对于接受干预的学校，平板电脑使学生的学习成绩平均降低了 75 分

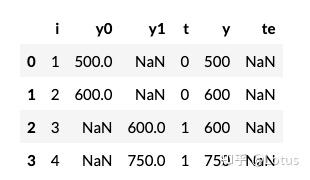
以上是假设，实际上我们无法观测到反事实的结果，如下。

我们还可以通过公式来理解为什么因果关系不等于相关关系。

相关关系如下

E[Y \mid T=1]-E[Y \mid T=0]

可以拆解为

\begin{array}{l}E[Y \mid T=1]-E[Y \mid T=0]=E\left[Y_{1} \mid T=1\right]-E\left[Y_{0} \mid T=0\right]+E\left[Y_{0} \mid T=1\right]-E\left[Y_{0} \mid T=1\right] \\ \text { } \\ E[Y \mid T=1]-E[Y \mid T=0]=\underbrace{E\left[Y_{1}-Y_{0} \mid T=1\right]}_{A T E T}+\underbrace{\left\{E\left[Y_{0} \mid T=1\right]-E\left[Y_{0} \mid T=0\right]\right\}}_{B I A S}\end{array}

我们直觉上的相关差异等于 被干预者 的 平均干预效果 + 偏差(bias)

偏差是由干预组和对照组在干预前的差异决定的，也就是说，如果他们都没有接受干预，差异会是多少