Matlab | Stackelberg斯塔克尔伯格模型求解及画图代码,阅完即可上手!
上一期给出了 古诺模型 的Matlab求解方法,本期给出Stackelberg模型的Matlab求解方法。
简单回顾下《微观经济学》中提到的古诺模型和Stackelberg模型的区别:
1. 古诺模型
市场背景:双/多寡头垄断 (竞争厂商在市场上的地位是平等的)
决策过程:同时决策 (甲决策时,并不知道乙的决策)
计算方法:同时求导 (两方程解两未知产量)
2. Stackelberg模型
市场背景:市场地位不平等 (存在 领导者 和 追随者 )
决策过程:序列决策 (预判 追随者 对己方决策的反应,然后调整初始决策以做出最终更优的决策)
计算方法:反/逆向归纳法 (先分析 追随者 的反应函数,然后把这个反应函数纳入 领导者 的决策过程,最终得到 领导者 的最优产量决策)
两种模型的差异细节不再过多赘述,简单来说:
古诺模型: 企业1和2地位平等,同时决策/求导;
Stackelberg模型: 企业1是领导者,企业2是追随者,序列决策/求导
一、求解Stackelberg模型
算例仍以上一期给出的 古诺模型 算例为基础,只不过现在 假设 企业1为领导者,企业2为追随者。
算例:
若市场需求函数为 p = a - b(q1 + q2) ,领导者企业1和追随者企业2的生产成本函数分别为 c1*q1 、 c2*q2^2 。求 Stackelberg均衡 ,并 计算利润。
由于企业1是领导者,所以企业1知道其制定初始产量决策后企业2的决策,并再次调整其产量决策。
如果不好理解以上逻辑,只需要记住,Stackelberg模型的序列求导指的是: 先对追随者的产量求导,带入领导者利润函数,再对领导者产量求导 。
因此,求解思路如下:
- 构建企业1和2的 利润函数 :价格×产量-成本;
- 对企业2产量q2 求导 ,令其=0并 求解 ;
- 将q2 代入 企业1的利润函数,并对q1 求导 ,令其=0后 求解 ;
- 将最优q1表达式 反代回 q2和企业1、2的利润表达式,得到 最优利润 。
以上四步的数学表达式和Matlab代码如下。
1. 构建企业1和2利润函数

对应的Matlab代码为:
syms a b q1 q2 c1 c2 % 定义参数/变量
Pi1 = (a - b*(q1 + q2))*q1 - c1*q1;
Pi2 = (a - b*(q1 + q2))*q2 - c2*q2^2; 可见,Matlab代码几乎是 照抄公式 ,只不过所有括号均需要用 小括号 ,时刻记得加上 乘号* 。
2. 对企业2的q2求导,令其=0并求解

对应的Matlab代码为:
equ2 = diff(Pi2, q2);
temp_q2 = solve(equ2, q2);Matlab的求导函数为 diff();解方程函数为solve()。 上述两行的含义分别为:
对利润函数Pi2中的q2变量求一阶导;求出来的表达式命名为equ2;
求解方程equ2=0中的q2,解出来的q2表达式命名为temp_q2。
3. 将q2代入Pi1,对q1求导,令其=0后求解

对应的Matlab代码为:
Pi1 = subs(Pi1, q2, temp_q2);
equ1 = diff(Pi1, q1);
Op_q1 = solve(equ1, q1);Matlab的替代函数为 subs() ,每行的含义分别为:
将Pi1中的q2的值替换为temp_q2的值,返回新的Pi1表达式;
对新的Pi1的q1求导,求导后的表达式命名为equ1;
求解方程equ1=0中的q1,该表达式就是最终企业1的最优产量决策。
至此,领导者企业1的最优产量已经得到,剩下的就是把Op_q1反代回之前的temp_q2、Pi1、Pi2表达式并化简。
4. 通过Op_q1反代,得到企业最优产量和利润
用Matlab求解古诺/Stackelberg模型最大 优势 其实就是这种 代入计算 。
若手算,Op_q1表达式已然较为繁琐, 代入利润函数表达式并化简的过程 ,非常花费时间,还容易计算错误。可若采用Matlab计算,代入仅需要 一行代码 即可。
Op_q2 = subs(temp_q2, q1, Op_q1);
Pi1 = subs(Pi1,q1, Op_q1);
Pi2 = subs(Pi2,{q1,q2}, {Op_q1,Op_q2});每行的含义分别为:
将temp_q2中的q1的值替换为Op_q1的值,返回最优企业2产量;
将Pi1中的q1替换为Op_q1(Pi1中已不包含q2,故无需替换);
将Pi2中的{q1, q2}分别替换为{Op_q1,Op_q2}的值。
如果此时直接查看各表达式值,看上去会很复杂,因为Maltab并不会自动帮我们化简。此时就需要调用化简函数。
Matlab化简函数 ,常见的有simplify、collect、expand、factor、subexpr、pretty等。
通常, simplify、collect和pretty 便可满足我们的绝大部分需求。
simplify(Op_q2);
simplify(Pi1);
simplify(Pi2);若想采用 所见即所得 的表现形式,调用pretty函数即可。

该形式易于抄写,非常直观。
更为方便的是,若 不想将公式手打入Word或Latex中 ,也可以调用Matlab中的latex()命令,将得到的结果复制粘贴到Word或Latex中。
具体方法在上一期 古诺模型 中有阐述,在此不再赘述。
至此,没动一次笔,便得到企业1和2的最优产量和利润表达式;同时,实现将表达式准确输入至Word中。 完美体现Matlab求解数学模型的优势 。
只要是 基于Stackelberg思想的数学模型 ,均可 自动化实现以上求解 。无非就是在第一步的时候,把利润函数改成 自己的研究问题 即可。
有兴趣的小伙伴也可以设定企业2为领导者,企业1为追随者进行求解。
二、画图
与上一期类似,可进行的数值分析有:
- 各企业最优产量(Op_q1和Op_q2)与各参数(a/b/c1/c2)关系图;
- 比较两企业最优产量的大小,计算市场占有率;
- 各企业最优利润与各参数关系;
- 比较两企业利润大小;
- 考察利润相同下,两个参数间的变化关系等;
为了表现 新的画图模式 ,本期展现如何画 双y轴图 和 子图 。
这里,仅 考察c2变化对两企业产量和利润的影响。
本期Stackelberg均衡解 下的最优产量和利润表达式 如下:
% 企业1最优产量和利润
Op_q1 = (a*b + 2*a*c2 - 2*b*c1 - 2*c1*c2)/(2*b^2 + 4*c2*b);
Pi1 = (a*b + 2*a*c2 - 2*b*c1 - 2*c1*c2)^2/(8*b*(b^2 + 3*b*c2 + 2*c2^2));
% 企业2最优产量和利润
Op_q2 = (a*b + 2*a*c2 + 2*b*c1 + 2*c1*c2)/(4*(b^2 + 3*b*c2 + 2*c2^2));
Pi2 = (a*b + 2*a*c2 + 2*b*c1 + 2*c1*c2)^2/(16*(b + c2)*(b + 2*c2)^2);在数值算例中,设a = 100, b = 1, c1 = 15。同时设c2取值范围为0到1,间隔0.03,即 c2 = [0: 0.03: 1] 。
注意: 每一个c2都对应一个Op_q1和一个Pi1,为计算所有c2对应的Op_q1和Pi1,写一个 循环 即可。
clear
a = 100; b = 1; c1 = 15;
c2 = [0: 0.03: 1];
for i = 1: length(c2)
Op_q1(i) = (a*b + 2*a*c2(i) - 2*b*c1 - 2*c1*c2(i))/(2*b^2 + 4*c2(i)*b);
Pi1(i) = (a*b + 2*a*c2(i) - 2*b*c1 - 2*c1*c2(i))^2/(8*b*(b^2 + 3*b*c2(i) + 2*c2(i)^2));
end很简单,只需要把 每个c2改为c2(i) 即可。因为c2不再是一个值,而是一系列的值,对应地,Op_q1变为Op_q1(i);Pi1变为Pi1(i)。
1. 双Y轴图
Matlab 双Y轴 的画图命令为 yyaxis left/right 。只需要在画图前激活左/右侧Y轴即可。其他命令与 上一期 类似,不再赘述。
yyaxis left % 激活左侧Y轴
plot(c2, Op_q1, '-bo', 'LineWidth', 2)
ylabel('企业1最优产量')
yyaxis right % 激活右侧Y轴
plot(c2, Pi1, '--r+', 'LineWidth', 2)
xlabel('企业2成本系数 c_2') % 横坐标
ylabel('企业1最优利润') % 纵坐标
legend('企业1产量','企业1利润'); % 图例
set(gca,'FontSize',15,'Fontname', 'Songti'); %统一设置图像格式
grid on % 画上横纵网格线若直接运行,可以画出如下图形。之所以选用蓝色、红色 画曲线 是因为 Matlab坐标轴文字和数字默认 使用了这两种颜色,仅是为了对应。
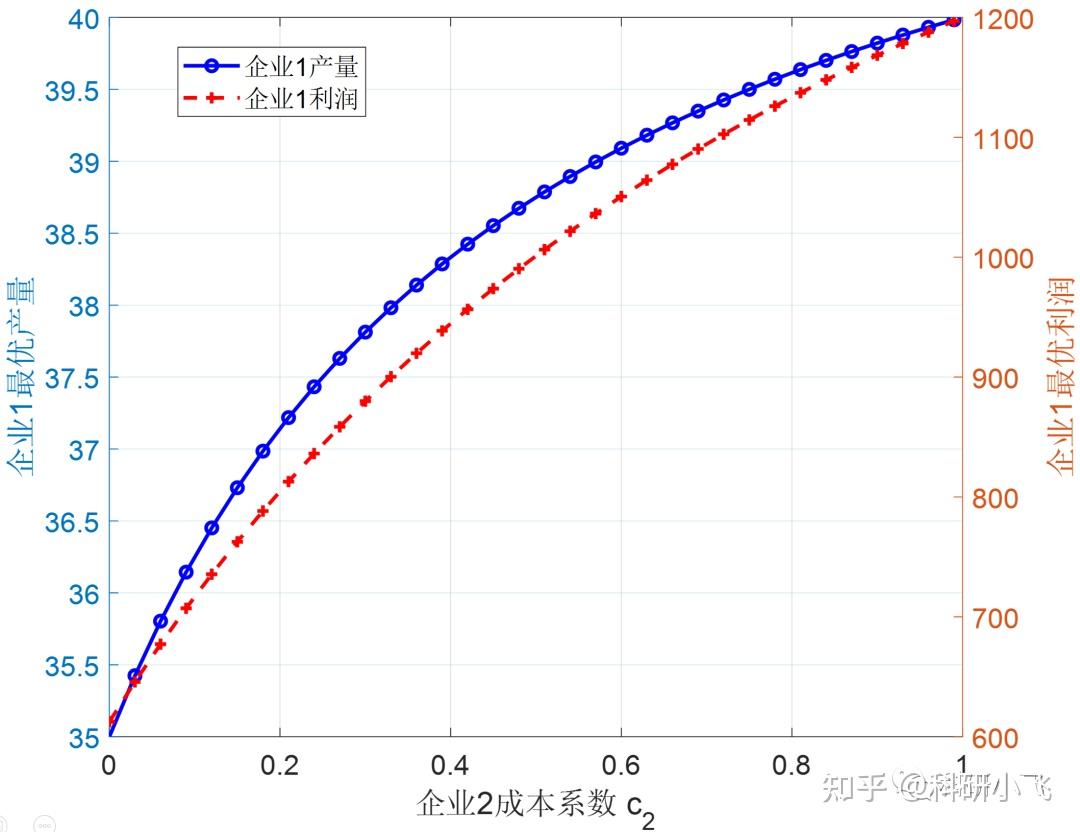
其中,‘ -bo ’含义是用蓝色(blue)的实线(-)连接,并在每个连接点上用圆圈(o)标记。‘ --r+ ’含义是用红色(red)的虚线(--)连接,并在每个连接点上用加号(+)标记。
实际上,写论文时尽量 避免使用颜色 ,因为论文黑白打印后无法区分颜色。所以,有必要修改下Matlab的 默认的双Y坐标值格式 。
仅针对双Y坐标值 修改颜色 的代码如下:
% 打开图,设置左右Y轴属性
fig = figure;
left_color = [0 0 0];
right_color = [0 0 0];
set(fig,'defaultAxesColorOrder',[left_color; right_color]);Matlab设置颜色采用 [r g b]格式 。其中,rgb对应 红绿蓝 ,取值范围均是 [0, 1] 。[1 0 0]代表红, [0 0 0]代表黑 。
再者,若PS中某颜色为[100,30,200],仅需要把每个数值除以255即可转化为[0,1]的值。更为特殊的 其他颜色 可查表获得(表格截图放在了文章最后)。
基于此,便可以画出全为(包含坐标值和曲线)黑色的图形。接下来, 介绍子图的画法 。
2. 子图
Matlab 子图 的画图命令为 subplot() 。subplot(1, 2, 1)的含义为:画1行2列排版下的第1个图形。
子图1绘制企业1的最优产量和利润图,子图2绘制企业2的,结果如下。
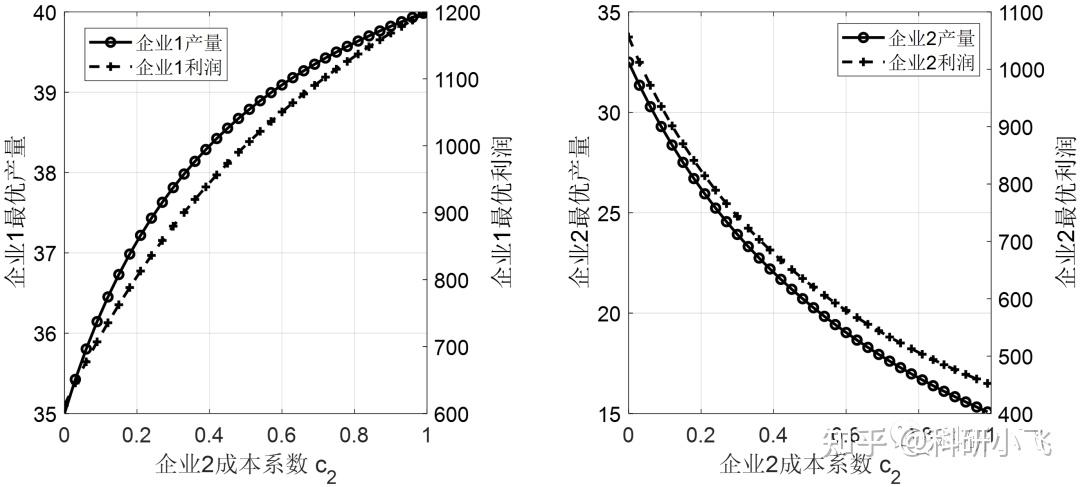
对应的Maltab代码其实是以上过程的简单重复,列在下面,仅供参考。
% 画第一个子图
subplot(1,2,1)
for i = 1: length(c2)
Op_q1(i) = (a*b + 2*a*c2(i) - 2*b*c1 - 2*c1*c2(i))/(2*b^2 + 4*c2(i)*b);
Pi1(i) = (a*b + 2*a*c2(i) - 2*b*c1 - 2*c1*c2(i))^2/(8*b*(b^2 + 3*b*c2(i) + 2*c2(i)^2));
yyaxis left % 激活左侧Y轴
plot(c2, Op_q1, '-ko', 'LineWidth', 2)
ylabel('企业1最优产量')
yyaxis right % 激活右侧Y轴
plot(c2, Pi1, '--k+', 'LineWidth', 2)
xlabel('企业2成本系数 c_2')
ylabel('企业1最优利润')
legend('企业1产量','企业1利润');
set(gca,'FontSize',15,'Fontname', 'Songti');
grid on % 画上横纵网格线
% 画第二个子图
subplot(1,2,2)
for i = 1: length(c2)
Op_q2(i) = (a*b + 2*a*c2(i) + 2*b*c1 + 2*c1*c2(i))/(4*(b^2 + 3*b*c2(i) + 2*c2(i)^2));
Pi2(i) = (a*b + 2*a*c2(i) + 2*b*c1 + 2*c1*c2(i))^2/(16*(b + c2(i))*(b + 2*c2(i))^2);
yyaxis left % 激活左侧Y轴
plot(c2, Op_q2, '-ko', 'LineWidth', 2)
ylabel('企业2最优产量')
yyaxis right % 激活右侧Y轴
