The family of Hall effect (霍尔效应家族汇总)
摘要
首先把“霍尔效应”当作固定宾语,按照“量子”,“自旋”,“反常”三个定语的排列,理论上一共有8种可能的组合(这里不讨论等价的“逆效应”(inverse)和复杂的分数(fractional)效应):
1.霍尔效应 Hall effect
2.反常霍尔效应 Anomalous Hall effect
3.自旋霍尔效应 Spin Hall effect
4.量子霍尔效应 Quantum Hall effect
5.量子反常霍尔效应 Quantum Anomalous Hall effect
6.量子自旋霍尔效应 Quantum Spin Hall effect
7.反常自旋霍尔效应 Anomalous Spin Hall effect
8.量子自旋反常霍尔效应 Quantum Anomalous Spin Hall effect (好长=。=)
但是这八种组合,从物理意义上来说不一定都是“有道理的”,比如最后两种。原因我直接贴维基的原文 [1] “The spin Hall effect belongs to the same family as the Anomalous Hall effecta, known for a long time in ferromagnets, which also originates from spin-orbit interaction“ 还有:“No magnetic field is needed for spin Hall effect. However, if a strong enough magnetic field is applied in the direction perpendicular to the orientation of the spins at the surfaces, spins will precess around the direction of the magnetic field and the spin Hall effect will disappear.”。换句话说,anomalous 在自旋面前显得“多余”。所以一般常见的名词是前六种。最后,如果仅仅把不需要磁场的就归为“反常”,反常霍尔效应更像是一个小家族,比如QAHE也可归为反常霍尔家族下,且反常霍尔效应原理上和其他的比如自旋霍尔效应有一定相似之处。
1.霍尔效应 Ordinary Hall effect
横向电流(电场)和纵向电压(纵向电流)的“转化”。
由于电子在磁场中受到洛伦兹力,其classical motion为绕着磁场打转,cyclotron frequency为 \omega_B=eB/m
在Drude model下,可以解得其纵向电阻率是个和磁场无关的常量 \rho_{xx}=E_x/j_x=m/ne^2\tau
而横向电阻率和relaxation time \tau 无关且正比于磁场 \rho_{xy}=E_y/j_x=B/en
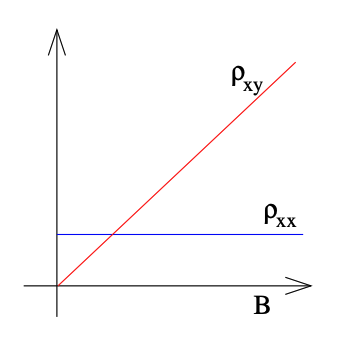
这里注意对于2D系统来说,电流密度是面密度,区别于3D的体密度。
于是对于横向电阻率来说,电阻和电阻率是一回事 \rho_{xy}=R_{xy} 。对于纵向电阻率和电阻的转化,则需要乘上一个无量纲的几何因子。
2.反常霍尔效应 Anomalous Hall effect
不需要磁场就能实现的霍尔效应。自然想到要在磁性材料中实现。铁磁材料居里温度以下具有自发磁矩,对于顺磁材料则需要外加磁场形成磁化M,在顺磁材料中,外加磁场和M的霍尔电流贡献常可以轻易分离,实验上问题并不大。而且反常霍尔效应的贡献一般比(正常)霍尔效应大。那磁化M如何造成霍尔效应呢? 一般来说分两种,一种是自旋依赖的散射(extrinsic)另一种是Berry curvature(intrinsic)带来的。对于后者,常常指metallic 体系即费米能级处于conduction band。如果费米能级处于gap中,则Berry curvature贡献的霍尔电导是quantized的,对应QAHE。更多细节可参考反常霍尔效应的RMP文章 [2] 。总之反常霍尔效应是个小家族,具体情况得具体分析。以下知乎文章有较为详细的解释:
3.自旋霍尔效应 Spin Hall effect
横向电流(电场)和纵向自旋流的“转化”。自旋流和电流(charge current)关系不再赘述。这里SHE一般指的是纵向无电压(或无charge current),而有自旋流(两侧反号的自旋累积)。机理这里直接引用T. Jungwirth大佬的RMP [3] :spin-dependent asymmetric deflection is observed in electron beams in vacuum due to Mott scattering (Mott, 1929, 1932; Shull, Chase, and Myers, 1943; Gay and Dunning, 1992). (ii) Mott’s skew scattering is regarded among the origins of the AHE of electron carriers in FM。只不过铁磁中两种自旋数目不相等,纵向还是会形成电流(反常霍尔效应)。而在具有自旋轨道耦合的非磁材料(NM)中则形成(自旋霍尔效应)。至于skew scattering的过程具体可以参考Mott 1929和1932年的文章或者上述专栏的文章。
4.量子霍尔效应 Quantum Hall effect
In 1980, Klaus von Klitzing 在低温强磁场下发现横向电阻率随着磁场增大具有量子化的平台,且纵向电阻率在平台处会降为零。此为量子霍尔效应,或整数霍尔效应。他也因此获得了1985年的诺贝尔物理学奖。

可以看到在低磁场下,横向电阻正比于磁场而纵向电阻率大致是一个常量,符合之前的经典计算。但是随着磁场增大,横向电阻率不再是霍尔效应中简单的线性关系,而是会出现出现量子化平台 \rho_{xy}=\frac{h}{e^2}\frac{1}{\nu} 。且处在平台时的状态,纵向电阻率为零。但这不意味着此时材料纵向是一个完美导体,相反,此时材料是一个绝缘体insulator,因为是此时纵向电导率也为零。以二维情况为例,此时电导率和电阻率不再是简单的倒数关系,而是矩阵(2x2矩阵)的逆的关系。可以看到,在 \rho_{xx}=\rho_{yy}=0 时, \sigma_{xx}=\sigma_{yy}=0 也为零(在 \rho_{xy} 处于平台且不为零时成立)。David Tong的QHE讲义里给了一个很好的物理图像来理解此时的情况 [4] :在Drude model 中,在relaxation time \tau\rightarrow \infty 时,即无杂质散射的情况下,纵向电流会被全部转化为横向电流。这对应着 \sigma_{xx}=0 (Drude模型里横向电阻率反比于relaxation time)。而这是个无耗散的过程 E_x \cdot J_y=0 (洛伦兹力不做功),对应着 \rho_{xx}(\tau\rightarrow \infty)=0 。

量子霍尔效应的机理可以由朗道能级(Landau levels)来解释。朗道能级的具体推导可见维基 [5] 或者David Tong的讲义。总的来说,自由电子在磁场下的能量本征值可以由引入产生湮灭算符来解,类似于谐振子。而对于本征态波函数来说,则是依赖于规范选取的(这是因为哈密顿量里的磁矢势 A 本身就依赖于规范选取)。此时的波函数并不是gauge invariant的,也就不能想当然地认为其有描述电子位置的物理意义。David Tong的原话是:“You shouldn’t read too much into this other than the fact that the profile of the wavefunctions is not telling us anything physical as it is not gauge invariant.”
回到本征值能量,即朗道能级上,无论用landau gauge还是symmetric gauge,利用各种技巧都可以解出其本征值都是: E_n=\hbar \omega_B(\nu+\frac12) ,且每个朗道能级具有相同的简并度 D=eBL_xL_y/h 。注意这里并没有考虑自旋。关于自旋和各种gauge及简并度的细节推导,可以参看David Tong的讲义。

于是自然的,我们可以推测或者想到,朗道能级 E_n=\hbar \omega_B(\nu+\frac12) 里的整数filling factor \nu 和QHE \rho_{xy}=\frac{h}{e^2}\frac{1}{\nu} 里的的整数 \nu 是同一个整数。事实上,如果我们从原先的经典理论出发, \rho_{xy}=B/en 并要求这个电阻率是量子的就会得到一个关于电子的密度 n 的等式 n=B\nu/\Phi_0 。这里quantum flux定义为: \Phi_0=h/e 。另一方面,从朗道能级的简并度 D=BL_xL_y/\Phi_0 出发可以得知, 这正好就是 \nu 个填充的朗道能级下系统的电子密度!
从朗道能级的结果中可知,能隙 \hbar \omega_B 正比于磁场。随着磁场的减小,能隙逐渐减小,于是在费米能级 E_f 下被占据的能带数越来越多,对应着 \nu 越来越大。但是这并不能解释在 B\neq\nu\Phi_0 时,即不是 \Phi_0 的整数倍的情况下为什么会出现平台。实际上,这里面杂质(disorder)扮演着十分重要的作用。换句话说,QHE的实现,依赖于材料的杂质(clean but not that clean)。由杂质引入的随机势使得朗道能级不再是一个个平带,而有一定的拓宽,且电子会被strongly localized (Anderson localization)。只有在能带中心附近才有extended states, 而大部分是localised state,不贡献电导。所以这解释了为什么 B\neq\nu\Phi_0 时会出现量子化平台:只有跨越了一个朗道能级中间的extended state,才能对电导有贡献。

维基上有一个很好的动画解释了这一过程 [6] :
简单的来说,杂质的作用就是在朗道能级没有刚好填充满的时候localize住电子,使得出现量子化平台。于是我们可以想到,在不破坏样品的前提下,杂质越多,平台越“平”。那么,如果杂质越少呢?会不会有越来越多的分数化平台出现对应分数量子霍尔效应?实际上,FQHE甚至可以不需要杂质,且对“分数”也有着一定的要求(不是任意的有理数都行)。更一般地,对于横向电场纵向电流这种特殊的“响应”,实际上可以用Chern-Simons 场论来描述。在那里电荷会和磁场flux有一个绑定,在某种意义上形成复合粒子composite particle,可以用来解释FQHE。
回到QHE,在边界上的robust的chiral edge state,属于extended states之一,且是一定会有的extended state。至于微观细节,外加电场后如何形成横向电流并具有量子化的电导,一般在朗道规范下来理解。本质上可以理解为不断增大的电磁势会不断改变电子波函数中心的位置,从而形成一个adiabatic pump。此即为著名的"Laughlin argument” [7] 。这里不再展开,详见我另一篇知乎文章。
关于边界态,可以如下定性解释和定量计算:电子在强磁场中进行的回旋运动,显然在边界处电子无法完成一个周期的运动,而是会被边界反射回来,接着向前运动。于是在上下两个边界,形成只朝一个方向运动的边界态(chiral edge state)。且这种边界态是不会被杂志破坏的(robust against impurity)。

考虑横向相反传播的上下两个边界态。此时纵向无电场,上下边界态化学势相等,相反传播的边界态电子数相等,横向无电流。此时在纵向上施加电场势必会造成上下两个边界态的的电子数不再相等,横向产生净电流。即完成了纵向电压转化横向电流的这一过程。至于为什么这个过程中的电导是量子化的,可以参见如下定量计算 [8] :(这里直接引用孙凯老师的讲义,公式3.54具有小笔误,问题不大)


由于每一个填充的朗道能级对应一对边界态,从而得到量子化电导率。且随着B增大,朗道能级填充数减小,电导率减小,电阻率增大。
5.量子反常霍尔效应和量子自旋霍尔效应 (QAHE & QSHE)
【5.1】 为啥把这两个放在一起讲,因为它们都和拓扑相关(更准确地说,前者对应Chern insulator,后者对应topological insulator),且彼此之间具有紧密的联系。
首先,贴出一个文章链接,很好地总结了Kane的RMP的TI的科普部分
其次,提到QAHE就不得不提到Haldane模型。所以我从这开始讲,具体模型的推导可以参看我之前的文章
或者看这个有Haldane本人亲自讲解视频的网站 Topology in condensed matter
网站上还有简洁的讲解和数学工具。以下也会用到上述网站的一些图片。
Haldane模型中的量子霍尔效应我更愿意称之为量子反常霍尔效应。原因是其机理和之前由朗道能级解释的量子霍尔效应不一样。其次虽然有用到磁场,但是是交错的,总的来说磁场为零。也就是说关键是打破时间反演对称性而不是磁场。但也不是说打破了时间反演对称性就一定是nontrivial的,由Haldane model的相图可知,只有描述时间反演对称性破缺的相关参数足够强才能得到非零陈数。
【5.2】 这里有个最关键的问题,为什么非零陈数(chern insulator)对应着量子反常霍尔效应(量子化电导率)?
这可以从几个方面入手。首先,根据我之前的Berry phase和Berry curvature的文章,在施加电场后,电子存在着一个和Berry curvature相关的反常速度:
v_n(k)=\frac{\partial\epsilon_n }{\hbar\partial k}-\frac{e}{\hbar}E\times\Omega_n(k)\\ \sigma_{xy}=\frac{e^2}{\hbar}\int_{BZ}dk^2\frac{\Omega_{kxky}}{2\pi^2}
纵向电导的计算有贝里曲率在布里渊区的积分给出。
其次,还可以从Bulk-boundary correspondence 来看,非零陈数和零陈数(真空)边界存在着chiral edge state for 2D(surface state for 3D)。这可以解释为band gap reopen的必然结果,其“中间态”为conducting state。

这个边界态的群速度恒正或恒负。边界态对应霍尔效应的原理上节描述QHE时有提到过,不再重复。以上大概解释了导致反常霍尔效应的机理。
【5.3】 然后就是为什么这个反常霍尔效应是量子的?
或者说,为什么贝里曲率在k空间的积分(除以2pi)是整数?除了我之前文章提到过的因为k空间具有周期性这样的不太令人满意的原因外,从物理上其实可以找到更多的诠释。
从石墨烯模型出发, H=h(k)\cdot \sigma , 这里向量 h(k) 是二维的,第三个分量为零,使得在k点和k'点处,线性色散关系对应无质量的狄拉克费米子,要想打开gap就必需得加入质量项,即非零的第三个分量。这里石墨烯哈密顿量的矩阵之所以是2x2的,是因为有A,B两个格子,这两个自由度类似于自旋所以也被称为赝自旋(pseudo-spin)。赝的意思来源于空间反演下A格子变到B格子,而“真”自旋空间反演不变。加入质量项的方法可以是仅引入A,B格子不同(相反)的在位势能,打破空间反演对称性。但发现这样对应的只是trivial insulator。接下来再打破时间反演对称性,引入不对称次近邻跃迁,就可以得到chern insulator。
Haldane model 的哈密顿量如下:
H(\mathbf{k}) = H_0(\mathbf{k})+ M\sigma_z + 2t_2\sum_i\,\sigma_z\,\sin(\mathbf{k}\cdot\mathbf{b}_i)\
再次强调这里的泡利矩阵只是为了不同sublattice的自由度。在时间反演操作下,k反号,泡利矩阵不变号,因此最后一项反号,不再具有时间反演对称性。
由Berry curvature的理论可知,形如 H=h(k)\cdot \sigma 这样的哈密顿量 [9] ,其贝里曲率的矢量形式(Berry flux)正比于 \hat{h}(k)=\frac{h(k)}{|h(k)|} ,是一个“磁单极子”所产生的磁场的形式。Berry flux类似于k空间的磁场。所以贝里曲率在整个参数区间的积分等于参数区间包含的Berry flux的源(磁单极子)的数目。注意这里的参数是三个,包含kx,ky和 \sigma_z 前乘的质量项参数。取定M,变化NNN hopping参数 t_2 ,在 \phi=\pi/2 下(这里的 \phi 指打破TRs的交错磁通带来NNN hopping所要附加的额外相位),我们可以画出这样的图 [10] :

这里平面坐标是kxky,纵坐标是质量项参数。在 t_2=0 时,仅仅破坏空间反演对称性,由计算得(计算过程略)贝里曲率在k和k'点反号,积分出反号的半个电导(陈数)相互抵消,体系trivial。随着 |t_2| 的增大,k点或k'点处的能隙闭合再重新打开。注意贝里曲率仅对有能隙的体系能定义,类似于不能再场点源处定义磁场(电场)大小。也就是说,band energy reopen 这一行为相当于引入了一个“磁单极子”使得k点和k'点的贝里曲率同号,贝里曲率在k平面的积分不再是零。
另外一个更为直白的解释是,如果我们在k和k'点处展开哈密顿量,并划分好布里渊区求出陈数我们会得到 [11] :
\\H_+=v(\delta k_x \sigma_x-\delta k_y \sigma_y)+m_+v^2\sigma_z\\ H_-=v(-\delta k_x \sigma_x-\delta k_y \sigma_y)+m_-v^2\sigma_z\\ n=\frac{sign(m_+)-sign(m_-)}{2}\\ m_{\pm}\propto M\mp3\sqrt{3}t_2\sin\phi
为了得到非零陈数,在k和k'点处得质量项 m_{\pm} 必须得反号。于是拓扑相变边界就由 M=\pm3\sqrt{3}t_2\sin\phi 所刻画。此时k或者k'点处质量项为零,能隙闭合。
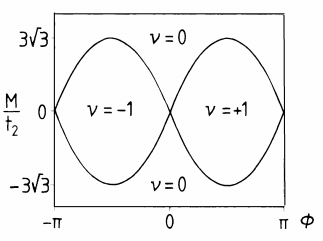
有一个点需要补充的是,由边界态的波函数对泡利算符做期望,算出来的结果告诉我们边界态是自旋极化的,有点类似于Rashba effect中的计算。边界态(表面态)的spin-momentum locking是很重要的一个性质。至此,相当于又把Haldane模型重讲了一遍......
【5.4】 但是故事还没结束。Haldane模型把磁场的需要做到了时间反演对称破缺的推广。尽管现在能够有方法去实现模型所需要的交错势能来实现QAHE,一个更推广的问题是,如果我们能在引入质量项的时候还能保持时间反演对称不变,会发生什么?
先不管如何实现,先来看看会发生什么:首先时间反演操作会让动量和自旋都反号。这就使得我们上文所描述的上下两个边界存在自旋相反流且传播方向也相反的流的图像不够。所以如果时间反演不变成立,对应的情况得是上下两个边界必须再各自增加一个流,自旋极化方向和传播方向与原有的都相反。如下图

此时,无论是上边界还是下边界,净电流(charge current)都为零,不存在QAHE,或者说相互抵消了。但存在净自旋流,即实现了量子自旋霍尔效应。
以上可以看出,量子自旋霍尔效应(Kane-Mele model)“相当于”两个Haldane模型的边界态的叠加。那么如何实现这种量子自旋霍尔效应呢?
首先我们得注意到Haldane模型中的质量项 2\sum_i\,\sigma_z\,\sin(\mathbf{k}\cdot\mathbf{b}_i)\ 之所以会打破时间反演对称是因为包含了动量k,其在时间反演操作下反号。要想不变号,那就得再乘一个在时间反演操作下变号的东西,也就是还没考虑的内禀自由度——自旋。而动量和自旋乘在一起就成了自旋轨道耦合(SOC)的形式(角动量里距离量纲可以吸收在自旋轨道耦合系数中)。这里给出Kane和Mele的原文章的分析 [12] :

这里矩阵变成了4x4的是因为,不再把k和k'点再单独分开写。这样加上不同sublattice直积起来一共四个自由度。泡利矩阵 \sigma_z 代表的是不同sublattice,泡利矩阵 \tau_z 代表的是k和k'点。在保持空间反演对称下(M=0),k和k'处质量项得反号,所以需要一个 \tau_z 矩阵。而SOC中的动量相对于对于不同sublattice也会反号,所以也需要一个 \sigma_z 。这样乘上自旋后,整个SOC项具有时间反演不变性(时间反演操作,交换k和k', \tau_z 和自旋出负号, \sigma_z 不需要变,仅仅描述不同sublattice,相当于 2\sum_i\,\sigma_z\,\sin(\mathbf{k}\cdot\mathbf{b}_i)\ 里 \sigma_z 不变,k的变化吸收到了 \tau_z 中)。
只要SOC足够强,让能带闭合再重新打开,实现能带反转,体系就也可以进到topologically nontrivial 的状态(QSHE),即拓扑绝缘体。不同于Chern insulator,TI的陈数是零。(但可以定义自旋陈数Spin Chern number [13] 如果体系自旋守恒的话。类似地如果晶体具有镜面对称性,还可以定义Mirror Chern number [14] 。这种利用晶体对称性(Topological crystalline insulator [15] )定义出“新”陈数的本质是对称性可以约化哈密顿量为block-diagonal。所以尽管总得陈数为零,由于分块了,总可以让它们相减得到新的指标。)
回到Ti上,我们需要新的方法来区分普通绝缘体和保持时间反演不变的拓朴绝缘体—— ℤ_2 拓扑不变量 [16] 。且这套方法可以拓展到3维的拓扑绝缘体。一般来说二维布里渊区有四个时间反演不变点 time-reversal invariant momentum(TRIM) points,而三维布里渊区有八个。推广到三维后还可以利用这八个点的对称性分类出强拓扑绝缘体(against perturbation)和弱拓扑绝缘体 [17] 。此外Wilson Loop [18] (瓦尼尔函数心缠绕)也是一个计算 ℤ_2 拓扑不变量的方法这里就不再展开。
最后,通过以上的分析,我们并不能就直接说QSHE和2D topological insulator 严格等价。要想在helical state上定义出自旋陈数我们默认了体系自旋守恒这一条件。然而这一条件并不总是满足(但依然可以定义 ℤ_2 拓扑数)。具体分析可以看如下回答。
【5.5】总结一下:在时间反演不变的具有强自旋轨道耦合的拓扑绝缘体中,可以实现QSHE。
但石墨烯的SOC比较弱,难实现QSHE。2007年,S.C.Zhang等人在实验上观察到了量子自旋霍尔效应(CdTe/HgTe/ CdTe量子阱,含有自旋轨道耦合较强的重金属元素) [19] 。
QSHE的边界态包含传播方向相反自旋极化相反的两个流,因此如果要发生背散射,必然存在自旋翻转,这在保持时间反演对称性下是禁止的(受到时间反演对称性保护 [20] ),因此,实现QAHE除了设计出Haldane模型的交错势, 另有一个方法就是在拓扑绝缘体中磁性参杂,破环时间反演对称性,抑制一个自旋通道。如若在磁性参杂后体系拓扑性质未被破坏,则有可能实现QAHE 。

此外,由于QAHE不依赖于载流子的电荷性,因此无论对于电子还是空穴,QAHE给出相同的电导,而霍尔效应给出相反的电导。这是在实验上尽管加了磁场(To initialize magnetic moment),也可以用来区分两种贡献的方法。
2013年,在磁性(铬)参杂的Bi2Se3(Sb2Se3)拓扑绝缘体薄膜中,Qi-Kun Xue等人在实验上首先观察到了量子反常霍尔效应 [21] 。
经评论区提醒,最后再补充一个在谷电子学(Valleytronics)中经常提到的 谷霍尔效应。
首先能谷对应于k空间中能带的极值点,比如石墨烯就是k和k'点。由于不同能谷在k空间一般分离得较远,不会存在谷之间的散射,使得能谷能够成为一个较好的自由度。同样地类比实空间中不同sublattice的自由度,这个k空间的能谷自由度也是赝自旋性质。此外,有之前分析可知,在一定条件下,k和k'处的贝里曲率可以是相反的,这就意味着不同能谷处的电子会偏向不同的方向,这就是谷霍尔效应(类比于自旋霍尔效应,不同自旋偏向不同方向)。那么如何实现谷霍尔效应,如何激发不同谷处的电子呢?一个可行的方案是利用单层二硫化钼材料。2012年,Q.Niu等人首先证明了单层二硫化钼不同谷处的电子可以被不同的圆偏光激发 [22] 。二硫化钼不同于石墨烯,空间反演对称性被打破,能隙打开,在一定的外界条件下(磁场,电场,且保持单层的直接带隙)不同能谷处贝里曲率反号,利用旋光激发能谷电子,从而实现能谷霍尔效应。但是单层MoS2本征二维特性使激子(被激发的电子和留下的空穴形成电子-空穴对)能够稳定存在。所以实现的效应更准确地说是激子霍尔效应(Exciton Hall effect)。该效应于2017年被东京大学Yoshihiro教授团队从实验上验证 [23] 。

参考
- ^ https://en.wikipedia.org/wiki/Spin_Hall_effect
- ^ https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.82.1539
- ^ https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.87.1213
- ^ http://www.damtp.cam.ac.uk/user/tong/qhe/qhe.pdf
- ^ https://en.wikipedia.org/wiki/Landau_quantization
- ^ https://commons.wikimedia.org/w/index.php?title=File%3AQuantumHallEffectExplanationWithLandauLevels.ogv
- ^ https://journals.aps.org/prb/abstract/10.1103/PhysRevB.23.5632
- ^ http://www-personal.umich.edu/~sunkai/teaching/Fall_2013/phys620.html
- ^ https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.82.1959
- ^ https://topocondmat.org/w4_haldane/haldane_model.html#Intro
- ^ https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.61.2015
- ^ https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.95.226801
- ^ https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.97.036808
- ^ https://ocw.tudelft.nl/course-lectures/2-maxwells-equations-and-magnetic-circuits-2-2-2/
- ^ https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.106.106802
- ^ https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.95.146802
- ^ https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.98.106803
- ^ https://journals.aps.org/prb/pdf/10.1103/PhysRevB.89.155114
- ^ https://science.sciencemag.org/content/318/5851/766
- ^ https://topocondmat.org/w5_qshe/fermion_parity_pump.html
- ^ https://science.sciencemag.org/content/340/6129/167
- ^ https://www.nature.com/articles/ncomms1882
- ^ https://www.nature.com/articles/nmat4996?proof=t

