常用聚类算法
一、什么是聚类
1.1 聚类的定义
聚类(Clustering)
是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇,使得
同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大
。也即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
1.2 聚类和分类的区别
-
聚类(Clustering):是指把相似的数据划分到一起,具体划分的时候并不关心这一类的标签,目标就是把相似的数据聚合到一起,聚类是一种无监督学习(Unsupervised Learning)方法。 -
分类(Classification):是把不同的数据划分开,其过程是通过训练数据集获得一个分类器,再通过分类器去预测未知数据,分类是一种监督学习(Supervised Learning)方法。
1.3 聚类的一般过程
- 数据准备:特征标准化和降维
- 特征选择:从最初的特征中选择最有效的特征,并将其存储在向量中
- 特征提取:通过对选择的特征进行转换形成新的突出特征
- 聚类:基于某种距离函数进行相似度度量,获取簇
-
聚类结果评估:分析聚类结果,如
距离误差和(SSE)等
1.4 数据对象间的相似度度量
对于数值型数据,可以使用下表中的相似度度量方法。

Minkowski
距离就是
Lp
范数(
p≥1
),而
Manhattan
距离、
Euclidean
距离、
Chebyshev
距离分别对应
p=1,2,∞
时的情形。
1.5 cluster之间的相似度度量
除了需要衡量对象之间的距离之外,有些聚类算法(如层次聚类)还需要衡量
cluster
之间的距离 ,假设
C_i
和
C_j
为两个
cluster
,则前四种方法定义的
C_i
和
C_j
之间的距离如下表所示。

-
Single-link定义两个cluster之间的距离为两个cluster之间距离最近的两个点之间的距离,这种方法会在聚类的过程中产生链式效应,即有可能会出现非常大的cluster -
Complete-link定义的是两个cluster之间的距离为两个``cluster之间距离最远的两个点之间的距离,这种方法可以避免链式效应`,对异常样本点(不符合数据集的整体分布的噪声点)却非常敏感,容易产生不合理的聚类 -
UPGMA正好是Single-link和Complete-link方法的折中,他定义两个cluster之间的距离为两个cluster之间所有点距离的平均值 -
最后一种
WPGMA方法计算的是两个cluster之间两个对象之间的距离的加权平均值,加权的目的是为了使两个cluster对距离的计算的影响在同一层次上,而不受cluster大小的影响,具体公式和采用的权重方案有关。
二、数据聚类方法
数据聚类方法主要可以分为
划分式聚类方法(Partition-based Methods)
、
基于密度的聚类方法(Density-based methods)
、
层次化聚类方法(Hierarchical Methods)
等。
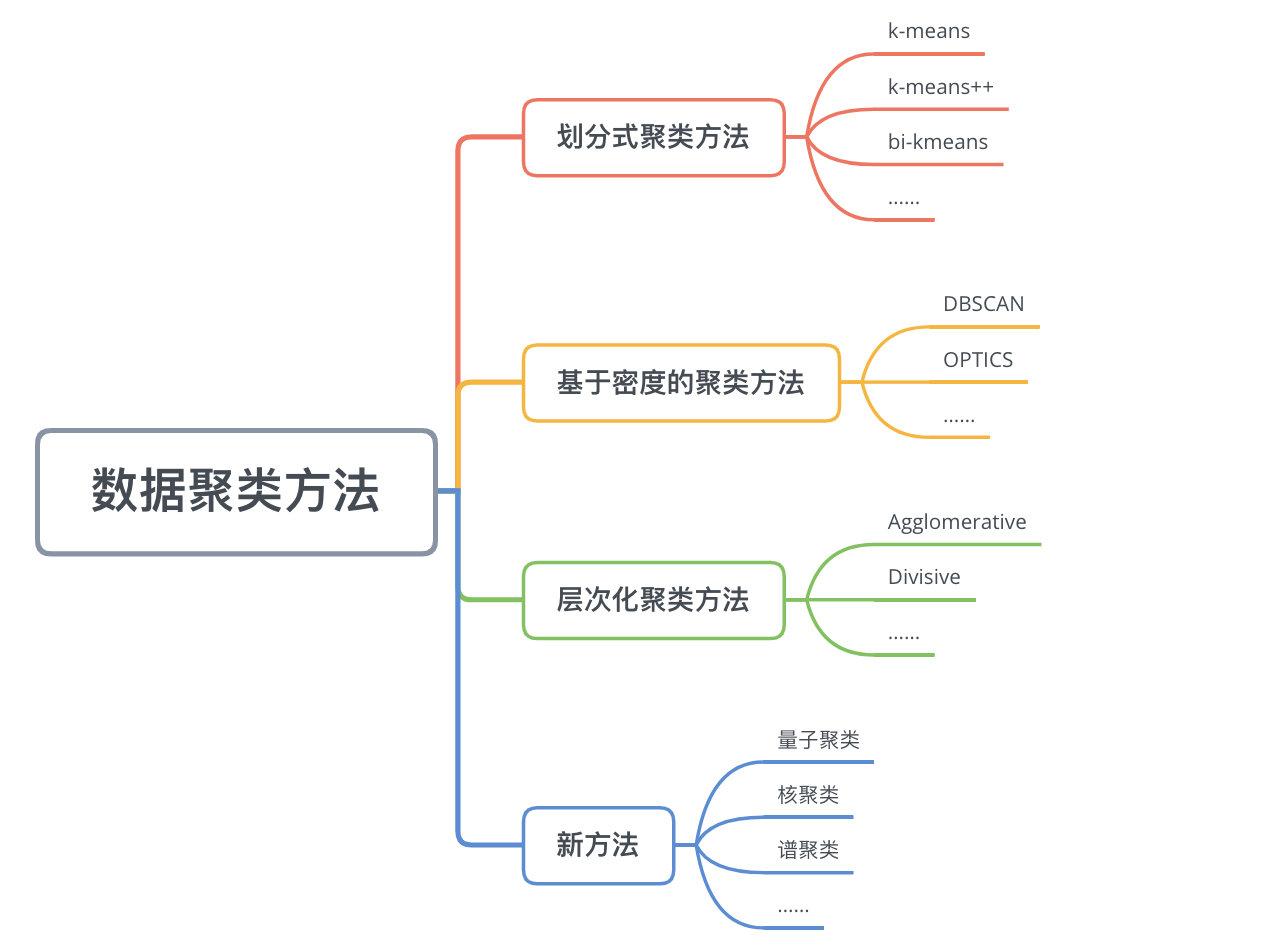
2.1 划分式聚类方法
划分式聚类方法需要事先指定簇类的数目或者聚类中心,通过反复迭代,直至最后达到"簇内的点足够近,簇间的点足够远"的目标。经典的划分式聚类方法有
k-means
及其变体
k-means++
、
bi-kmeans
、
kernel k-means
等。
2.1.2 k-means算法
经典的
k-means
算法的流程如下:

经典
k-means
源代码
,下左图是原始数据集,通过观察发现大致可以分为4类,所以取
k=4
,测试数据效果如下右图所示。
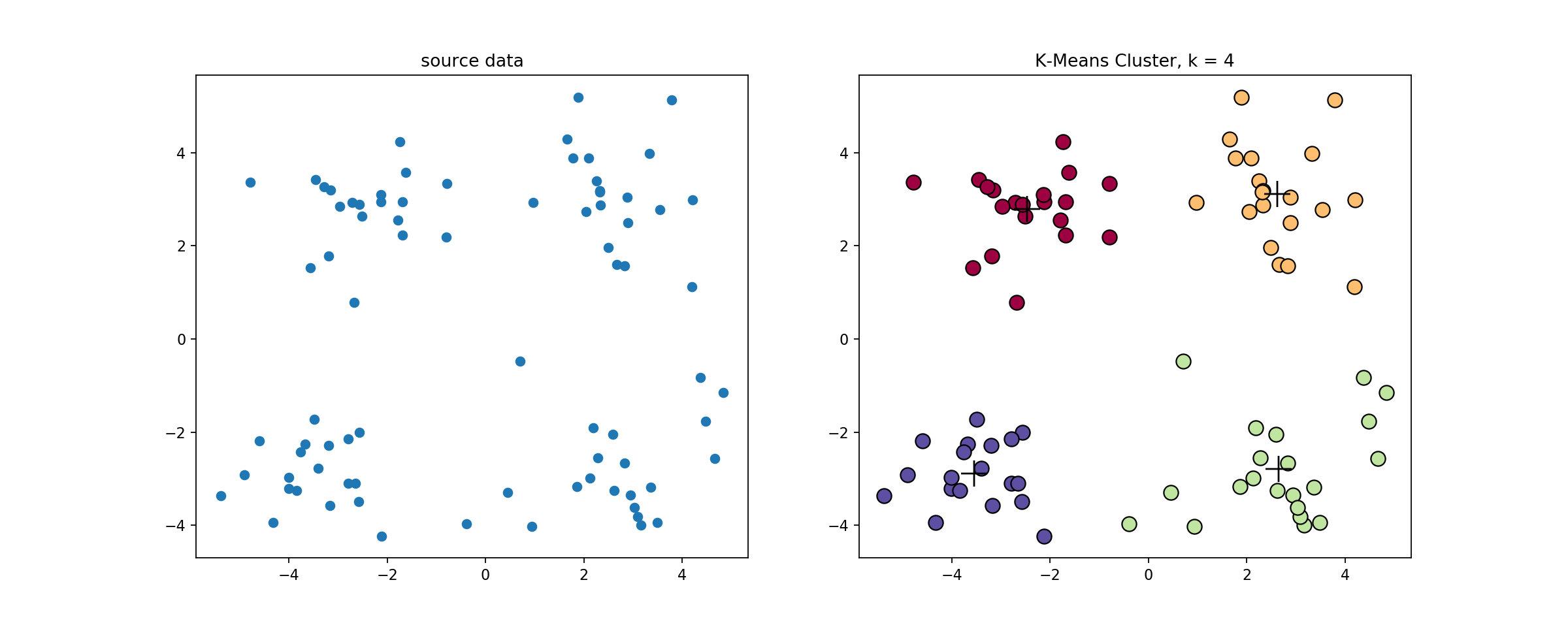

看起来很顺利,但事情并非如此,我们考虑
k-means
算法中最核心的部分,假设
x_i(i=1,2,…,n)
是数据点,
\mu_j(j=1,2,…,k)
是初始化的数据中心,那么我们的目标函数可以写成
\min\sum_{i=1}^{n} \min \limits_{j=1,2,...,k}\left |\left | x_i -\mu_j\right | \right |^2 \\
这个函数是 非凸优化函数 ,会收敛于局部最优解,可以参考 证明过程 。举个 , \mu_1=\left [ 1,1\right ] ,\mu_2=\left [ -1,-1\right ] ,则
z=\min \limits_{j=1,2}\left |\left | x_i -\mu_j\right | \right |^2 \\
该函数的曲线如下图所示

可以发现该函数有两个局部最优点,当时初始质心点取值不同的时候,最终的聚类效果也不一样,接下来我们看一个具体的实例。

在这个例子当中,下方的数据应该归为一类,而上方的数据应该归为两类,这是由于初始质心点选取的不合理造成的误分。而 k 值的选取对结果的影响也非常大,同样取上图中数据集,取 k=2,3,4 ,可以得到下面的聚类结果:
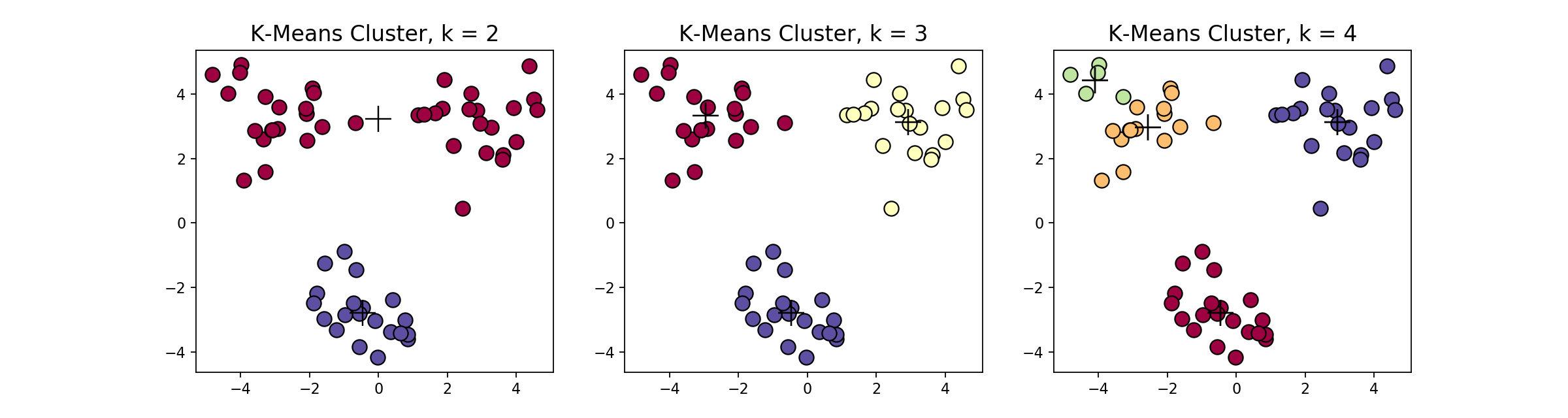
一般来说,经典
k-means
算法有以下几个特点:
- 需要提前确定 k 值
- 对初始质心点敏感
- 对异常数据敏感
2.1.2 k-means++算法
k-means++
是针对
k-means
中初始质心点选取的优化算法。该算法的流程和
k-means
类似,改变的地方只有初始质心的选取,该部分的算法流程如下

k-means++
源代码
,使用
k-means++
对上述数据做聚类处理,得到的结果如下
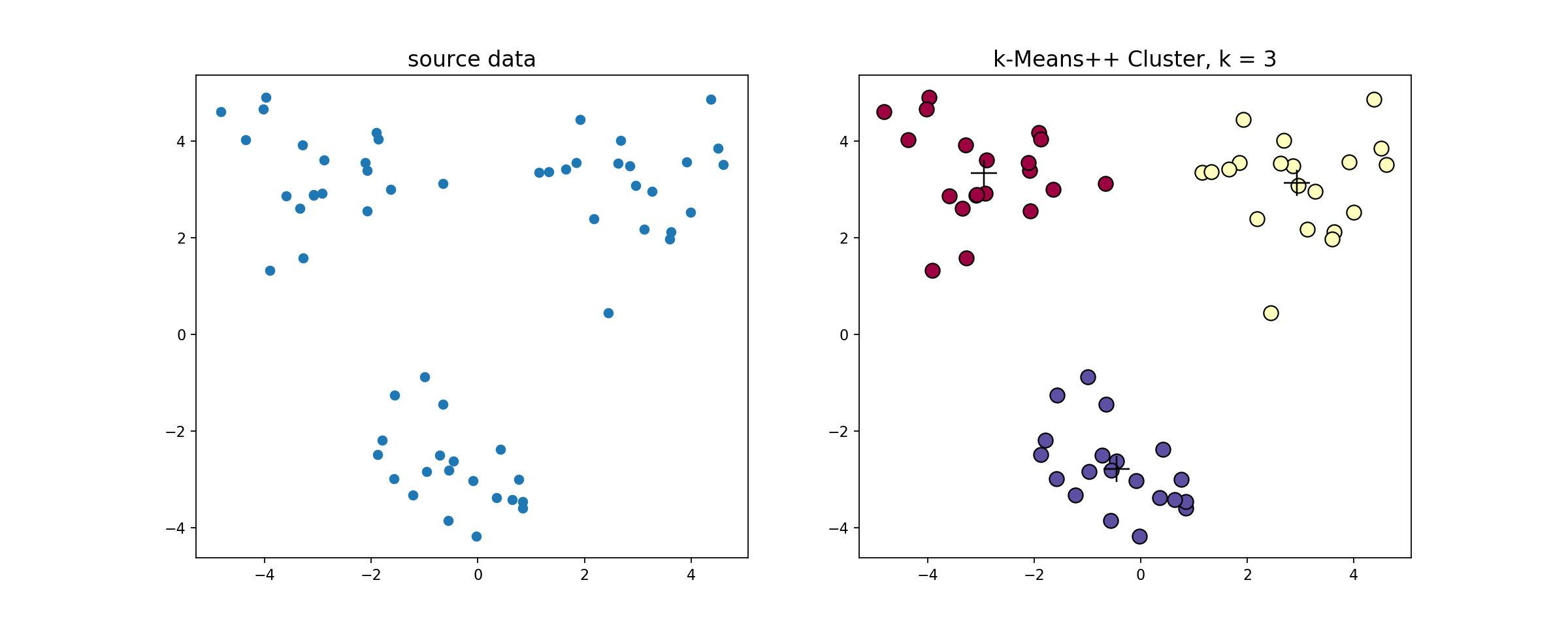
2.1.3 bi-kmeans算法
一种度量聚类效果的指标是
SSE(Sum of Squared Error)
,他表示聚类后的簇离该簇的聚类中心的平方和,
SSE
越小,表示聚类效果越好。
bi-kmeans
是针对
kmeans
算法会陷入局部最优的缺陷进行的改进算法。该算法基于SSE最小化的原理,首先将所有的数据点视为一个簇,然后将该簇一分为二,之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否能最大程度的降低
SSE
的值。
该算法的流程如下:

bi-kmeans
算法
源代码
,利用
bi-kmeans
算法处理上节中的数据得到的结果如下图所示。

这是一个全局最优的方法,所以每次计算出来的
SSE
值基本也是一样的(
但是还是不排除有部分随机分错的情况
),我们和前面的
k-means
、
k-means++
比较一下计算出来的
SSE
值

可以看到,
k-means
每次计算出来的
SSE
都较大且不太稳定,
k-means++
计算出来的
SSE
较稳定并且数值较小,而
bi-kmeans
4次计算出来的
SSE
都一样,并且计算的
SSE
都较小,说明聚类的效果也最好。
2.2 基于密度的方法
k-means
算法对于凸性数据具有良好的效果,能够根据距离来讲数据分为球状类的簇,但对于非凸形状的数据点,就无能为力了,当
k-means
算法在环形数据的聚类时,我们看看会发生什么情况。

从上图可以看到,
kmeans
聚类产生了错误的结果,这个时候就需要用到基于密度的聚类方法了,该方法需要定义两个参数
\varepsilon
和
M
,分别表示密度的邻域半径和邻域密度阈值。
DBSCAN
就是其中的典型。
2.2.1 DBSCAN算法
首先介绍几个概念,考虑集合 X=\left \{x^{(1)},x^{(2)},...,x^{(n)}\right \} , \varepsilon 表示定义密度的邻域半径,设聚类的邻域密度阈值为 M ,有以下定义:
- \varepsilon 邻域( \varepsilon -neighborhood)
N_{\varepsilon }(x)=\left \{y\in X|d(x, y) < \varepsilon \right \} \\
- 密度(desity) x 的密度为
\rho (x)=\left | N_{\varepsilon }(x)\right | \\
- 核心点(core-point)
设 x\in X ,若 \rho (x) \geq M ,则称 x 为 X 的核心点,记 X 中所有核心点构成的集合为 X_c ,记所有非核心点构成的集合为 X_{nc} 。
- 边界点(border-point)
若 x\in X_{nc} ,且 \exists y\in X ,满足
y\in N_{\varepsilon }(x) \cap X_c \\
即 x 的 \varepsilon 邻域中存在核心点,则称 x 为 X 的边界点,记 X 中所有的边界点构成的集合为 X_{bd} 。
此外,边界点也可以这么定义:若 x\in X_{nc} ,且 x 落在某个核心点的 \varepsilon 邻域内,则称 x 为 X 的一个边界点,一个边界点可能同时落入一个或多个核心点的 \varepsilon 邻域。
- 噪声点(noise-point)
若 x 满足
x\in X,x \notin X_{c}且 x\notin X_{bd} \\
则称 x 为噪声点。
如下图所示,设 M=3 ,则A为核心点,B、C是边界点,而N是噪声点。

该算法的流程如下:

构建
\varepsilon
邻域的过程可以使用
kd-tree
进行优化,循环过程可以使用
Numba、Cython、C
进行
优化
,
DBSCAN
的
源代码
,使用该节一开始提到的数据集,聚类效果如下

聚类的过程示意图

当设置不同的 \varepsilon 时,会产生不同的结果,如下图所示

当设置不同的 M 时,会产生不同的结果,如下图所示
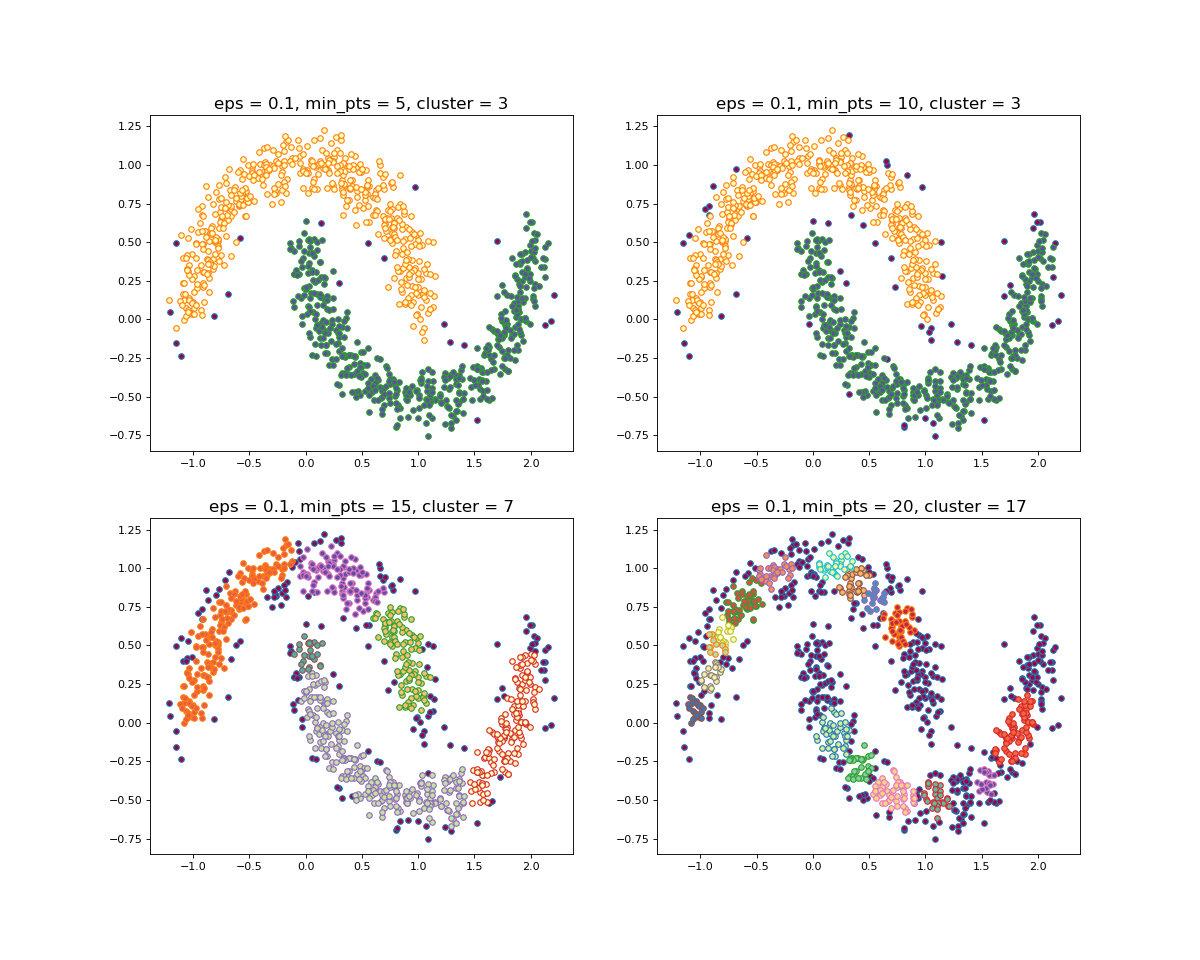
一般来说,
DBSCAN
算法有以下几个特点:
- 需要提前确定 \varepsilon 和 M 值
- 不需要提前设置聚类的个数
- 对初值选取敏感,对噪声不敏感
- 对密度不均的数据聚合效果不好
2.2.2 OPTICS算法
在
DBSCAN
算法中,使用了统一的
\varepsilon
值,当数据密度不均匀的时候,如果设置了较小的
\varepsilon
值,则较稀疏的
cluster
中的节点密度会小于
M
,会被认为是边界点而不被用于进一步的扩展;如果设置了较大的
\varepsilon
值,则密度较大且离的比较近的
cluster
容易被划分为同一个
cluster
,如下图所示。

-
如果设置的
\varepsilon
较大,将会获得A,B,C这3个
cluster -
如果设置的
\varepsilon
较小,将会只获得C1、C2、C3这3个
cluster
对于密度不均的数据选取一个合适的 \varepsilon 是很困难的,对于高维数据,由于 维度灾难(Curse of dimensionality) , \varepsilon 的选取将变得更加困难。
怎样解决
DBSCAN
遗留下的问题呢?
The basic idea to overcome these problems is to run an algorithm which produces a special order of the database with respect to its density-based clustering structure containing the information about every clustering level of the data set (up to a "generating distance" \varepsilon ), and is very easy to analyze.
即能够提出一种算法,使得基于密度的聚类结构能够呈现出一种特殊的顺序,该顺序所对应的聚类结构包含了每个层级的聚类的信息,并且便于分析。
OPTICS(Ordering Points To Identify the Clustering Structure, OPTICS)
实际上是
DBSCAN
算法的一种有效扩展,主要解决对输入参数敏感的问题。即选取有限个邻域参数
\varepsilon _i( 0 \leq\varepsilon_{i} \leq \varepsilon)
进行聚类,这样就能得到不同邻域参数下的聚类结果。
在介绍
OPTICS
算法之前,再扩展几个概念。
- 核心距离(core-distance)
样本 x∈X ,对于给定的 \varepsilon 和 M ,使得 x 成为核心点的最小邻域半径称为 x 的核心距离,其数学表达如下
cd(x)=\left\{\begin{matrix} UNDEFINED, \left | N_{\varepsilon }(x)\right |< M\\ d(x,N_{\varepsilon }^{M}(x)), \left | N_{\varepsilon }(x)\right | \geqslant M \end{matrix}\right. \\
其中, N_{\varepsilon }^{i}(x) 表示在集合 N_{\varepsilon }(x) 中与节点 x 第 i 近邻的节点,如 N_{\varepsilon }^{1}(x) 表示 N_{\varepsilon }(x) 中与 x 最近的节点,如果 x 为核心点,则必然会有 cd(x) \leq\varepsilon 。
- 可达距离(reachability-distance)
设 x,y∈X ,对于给定的参数 \varepsilon 和 M , y 关于 x 的可达距离定义为
rd(y,x)=\left\{\begin{matrix} UNDEFINED, \left | N_{\varepsilon }(x)\right |< M\\ \max{\{cd(x),d(x,y)\}}, \left| N_{\varepsilon }(x)\right | \geqslant M \end{matrix}\right. \\
特别地,当 x 为核心点时,可以按照下式来理解 rd(x,y) 的含义
rd(x,y)=\min\{\eta:y \in N_{\eta}(x) 且 \left|N_{\eta}(x)\right| \geq M\} \\
即 rd(x,y) 表示使得" x 为核心点"且" y 从 x 直接密度可达"同时成立的最小邻域半径。
可达距离的意义在于衡量 y 所在的密度,密度越大,他从相邻节点直接密度可达的距离越小,如果聚类时想要朝着数据尽量稠密的空间进行扩张,那么可达距离最小是最佳的选择。
举个 ,下图中假设 M=3 ,半径是 ε 。那么 P 点的核心距离是 d(1,P) ,点2的可达距离是 d(1,P) ,点3的可达距离也是 d(1,P) ,点4的可达距离则是 d(4,P) 的距离。

OPTICS
源代码
,算法流程如下:

算法中有一个很重要的insert_list()函数,这个函数如下:

OPTICS
算法输出序列的过程:

该算法最终获取知识是一个 输出序列 ,该序列按照密度不同将相近密度的点聚合在一起,而不是输出该点所属的具体类别,如果要获取该点所属的类型,需要再设置一个参数 \varepsilon'(\varepsilon' \leq \varepsilon) 提取出具体的类别。这里我们举一个例子就知道是怎么回事了。
随机生成三组密度不均的数据,我们使用
DBSCAN
和
OPTICS
来看一下效果。


可见,
OPTICS
第一步生成的输出序列较好的保留了各个不同密度的簇的特征,根据输出序列的可达距离图,再设定一个合理的
\varepsilon'
,便可以获得较好的聚类效果。
2.3 层次化聚类方法
前面介绍的几种算法确实可以在较小的复杂度内获取较好的结果,但是这几种算法却存在一个
链式效应
的现象,比如:A与B相似,B与C相似,那么在聚类的时候便会将A、B、C聚合到一起,但是如果A与C不相似,就会造成聚类误差,严重的时候这个误差可以一直传递下去。为了降低
链式效应
,这时候层次聚类就该发挥作用了。

层次聚类算法 (hierarchical clustering)
将数据集划分为一层一层的
clusters
,后面一层生成的
clusters
基于前面一层的结果。层次聚类算法一般分为两类:
-
Agglomerative 层次聚类
:又称自底向上(bottom-up)的层次聚类,每一个对象最开始都是一个
cluster,每次按一定的准则将最相近的两个cluster合并生成一个新的cluster,如此往复,直至最终所有的对象都属于一个cluster。这里主要关注此类算法。 -
Divisive 层次聚类
: 又称自顶向下(top-down)的层次聚类,最开始所有的对象均属于一个
cluster,每次按一定的准则将某个cluster划分为多个cluster,如此往复,直至每个对象均是一个cluster。
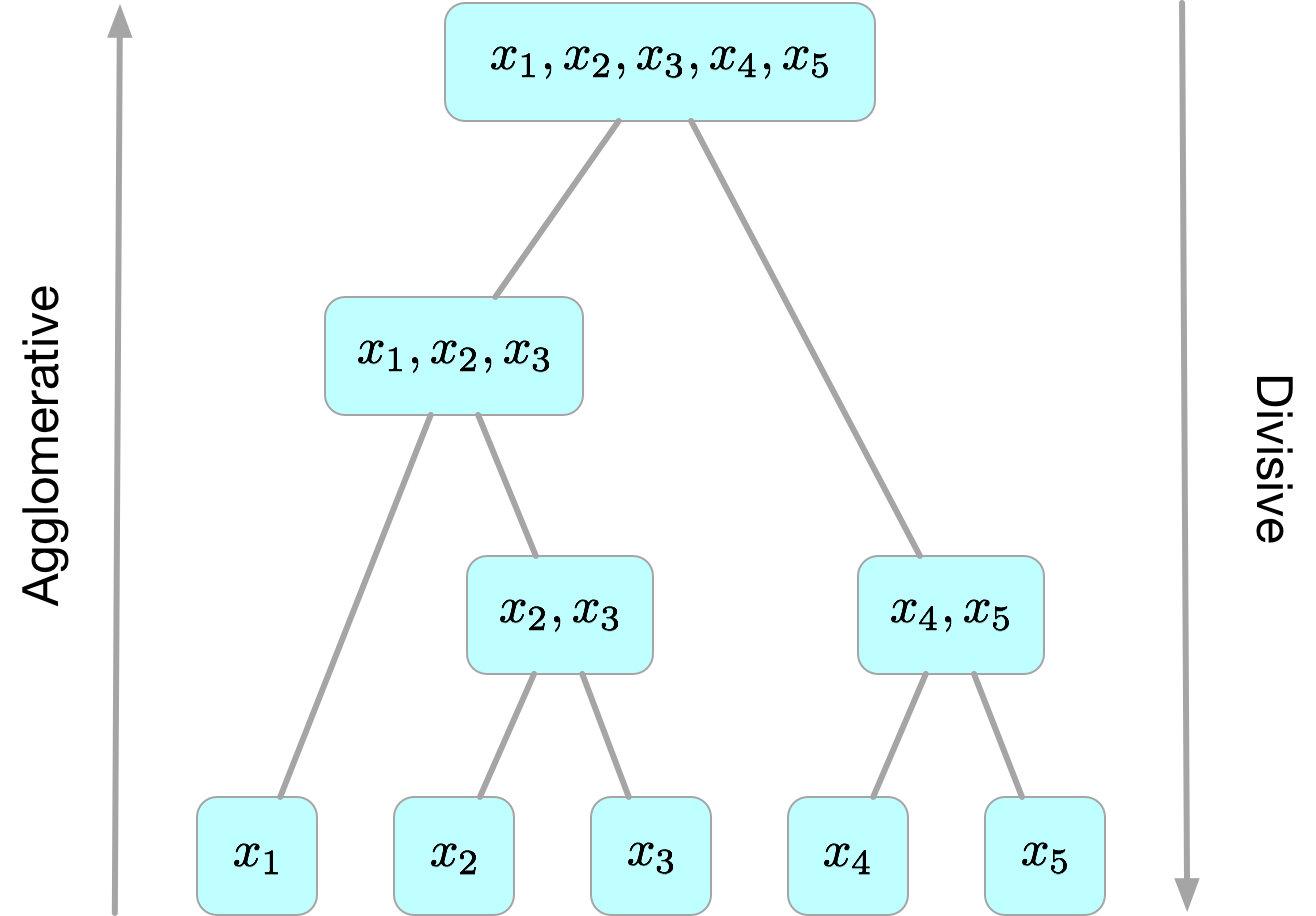
另外,需指出的是,层次聚类算法是一种贪心算法(greedy algorithm),因其每一次合并或划分都是基于某种局部最优的选择。
2.3.1 Agglomerative算法
给定数据集
X=\left \{x^{(1)},x^{(2)},...,x^{(n)}\right \}
,
Agglomerative
层次聚类最简单的实现方法分为以下几步:

Agglomerative
算法
源代码
,可以看到,该 算法的时间复杂度为
O(n^3)
(由于每次合并两个
cluster
时都要遍历大小为
O(n^2)
的距离矩阵来搜索最小距离,而这样的操作需要进行
n−1
次),空间复杂度为
O(n^2)
(由于要存储距离矩阵)。

上图中分别使用了层次聚类中4个不同的
cluster
度量方法,可以看到,使用
single-link
确实会造成一定的链式效应,而使用
complete-link
则完全不会产生这种现象,使用
average-link
和
ward-link
则介于两者之间。
2.4 聚类方法比较

三、参考文献
[1] 李航.统计学习方法
[2] Peter Harrington.Machine Learning in Action/李锐.机器学习实战
[3] https://www. zhihu.com/question/3455 4321
[4] T. Soni Madhulatha.AN OVERVIEW ON CLUSTERING METHODS
[5] https:// zhuanlan.zhihu.com/p/32 375430
[6] http://heathcliff.me/聚类分析(一):层次聚类算法
[7] https://www. cnblogs.com/tiaozistudy /p/dbscan_algorithm.html
[8] https:// blog.csdn.net/itplus/ar ticle/details/10089323
[9] Mihael Ankerst.OPTICS: ordering points to identify the clustering structure



